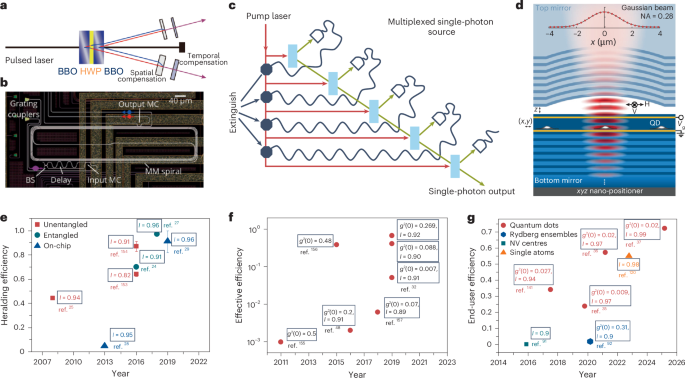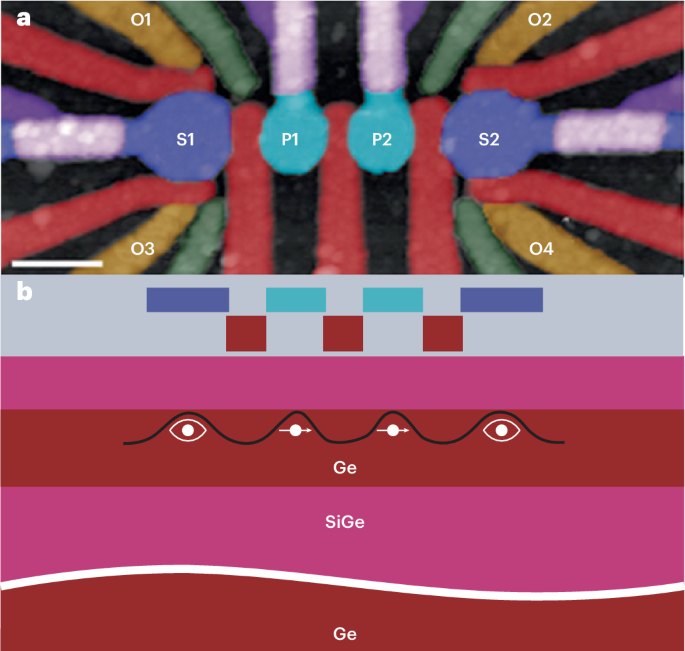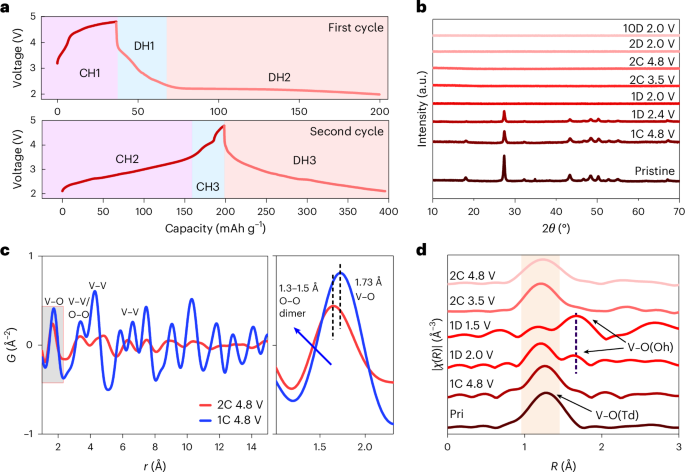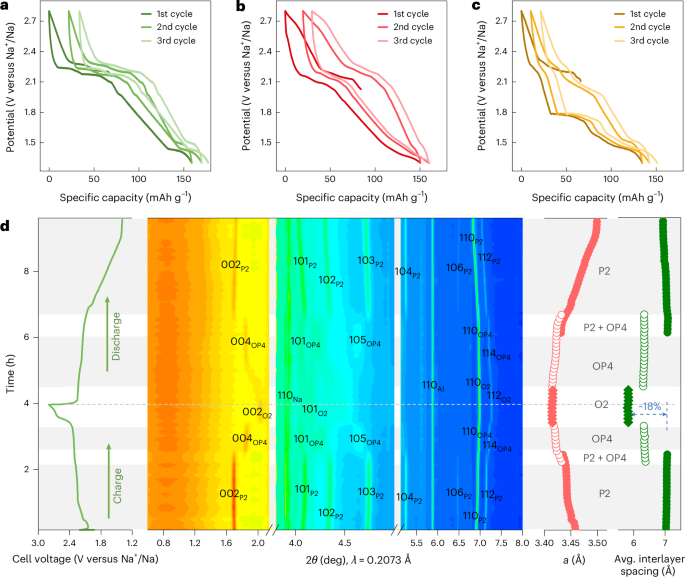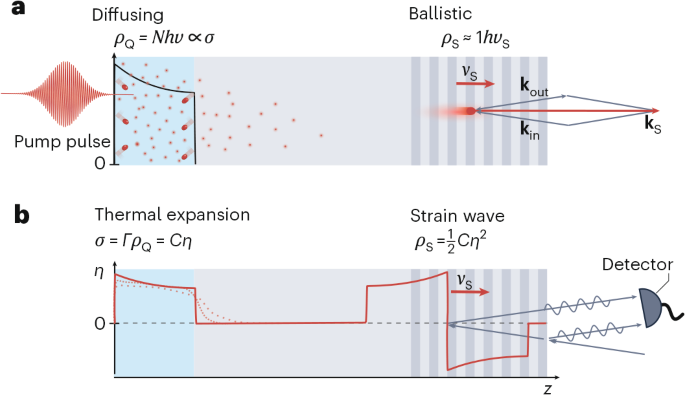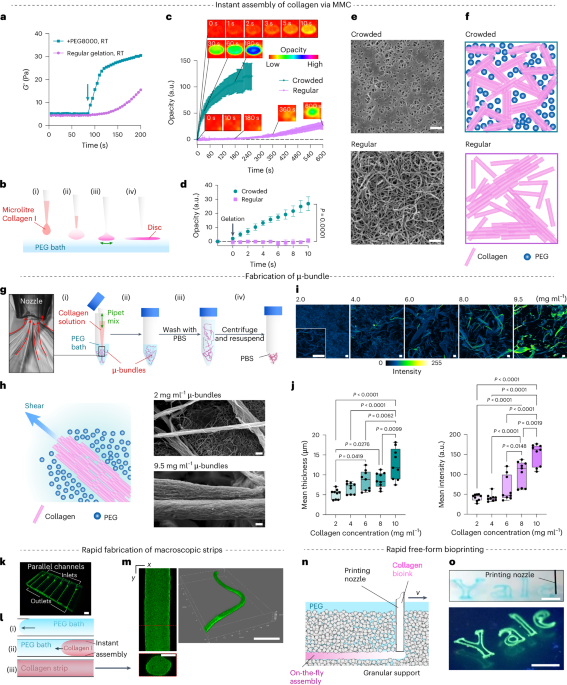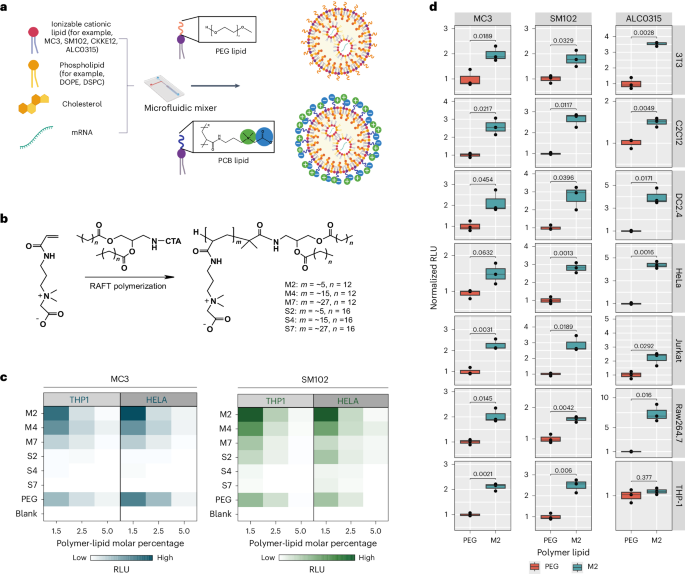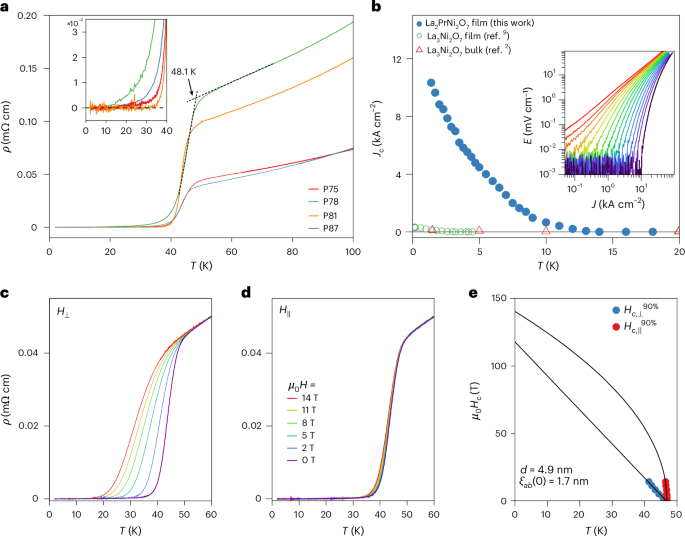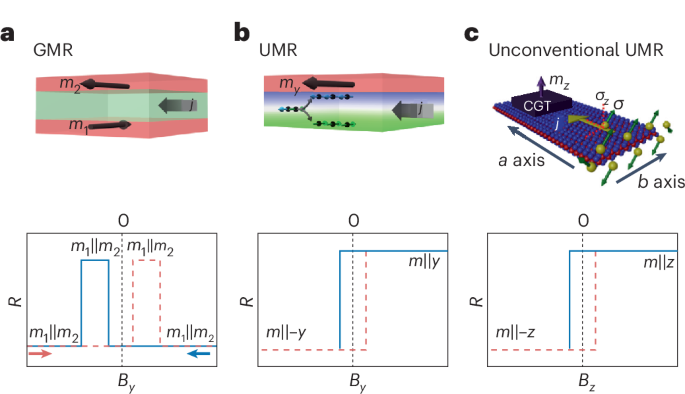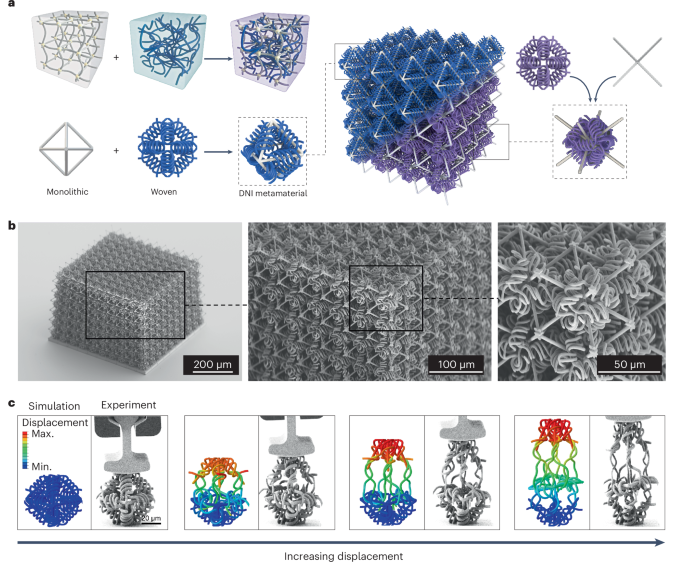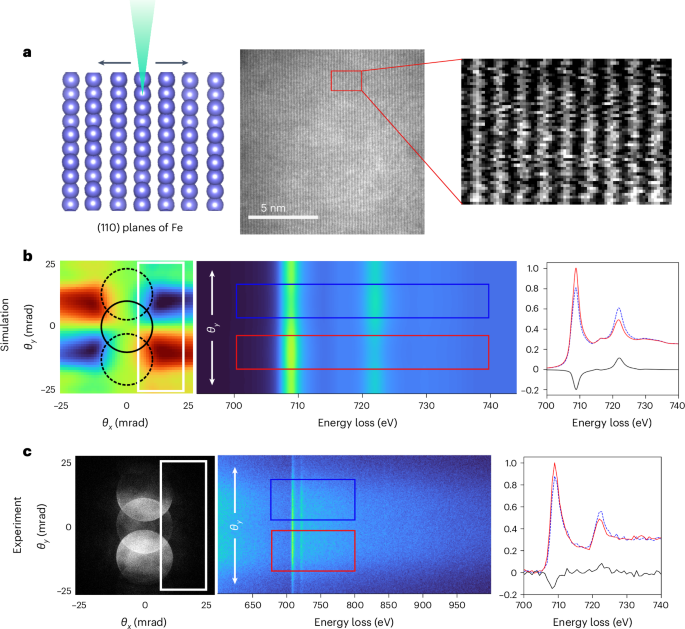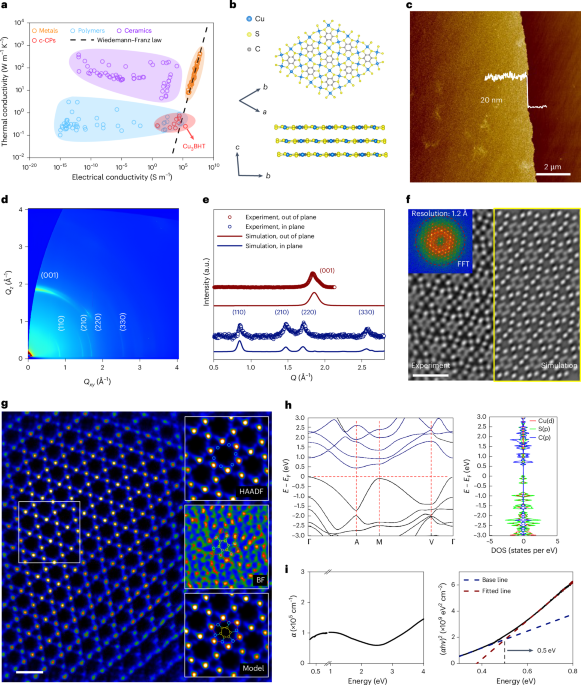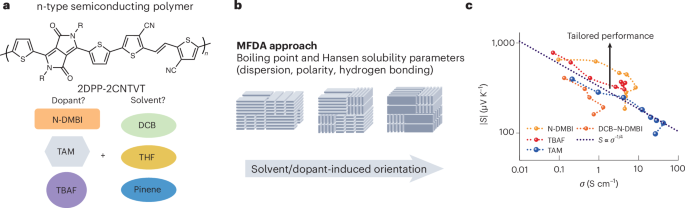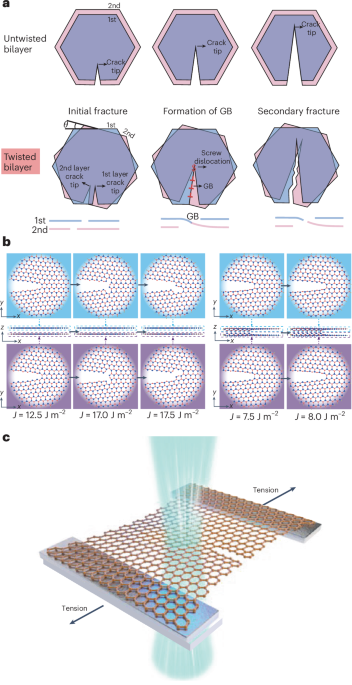
The Hall effect has been a powerful probe of the physics of materials for more than a century.
In the presence of a magnetic field, Edwin Hall (pictured) observed a transverse voltage when passing current through a metallic gold leaf, which can be attributed to the deflection of charge carriers due to the Lorentz force1. This Hall voltage can be used to determine the sign and concentration of charge carriers, and the magnitude of magnetic fields.
Credit: GL Archive / Alamy Stock Photo
Since this first observation in 1879, the range of materials exhibiting different types of Hall effect has increased dramatically. The anomalous Hall effect, which is a transverse voltage in the absence of an external magnetic field, was observed shortly after in ferromagnetic metals by Hall and more recently in antiferromagnets.
A remarkable milestone was the discovery of the integer quantum Hall effect by Klaus von Klitzing and colleagues, marking the entrance of the Hall effect into quantum territory2. At a semiconductor–oxide interface, where electrons are confined in the vertical direction but free to move in the other two directions (known as two-dimensional electron gases; 2DEGs), von Klitzing observed a Hall conductance only at certain stepwise values corresponding to integer values of the fundamental constants e2/h, where e is the elementary charge and h is Planck’s constant. This observation, which required very low temperatures (approximately 1.8 K) and very high magnetic fields (on the order of 15 T), led to von Klitzing being awarded the 1985 Nobel Prize in Physics.
Working on 2DEGs at even lower temperature (approximately 0.4 K), Horst Störmer and Daniel Tsui observed more stepwise changes in the Hall conductance, which could be accounted for as fractionalized values of e2/h (ref. 3). Robert Laughlin explained this effect in terms of fractionally charged quasiparticles, and these three scientists were awarded the 1998 Nobel Prize in Physics for their discovery of the fractional quantum Hall effect. In 2013, taking advantage of progress on the topological classification of materials, advances in the synthesis of these materials and theoretical guidance, a quantum anomalous Hall effect, which is the quantum Hall effect in the absence of an external magnetic field, was observed in thin films of a magnetically doped topological insulator4.
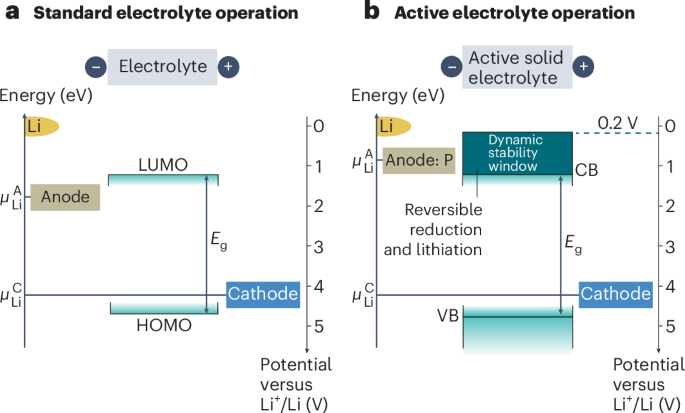
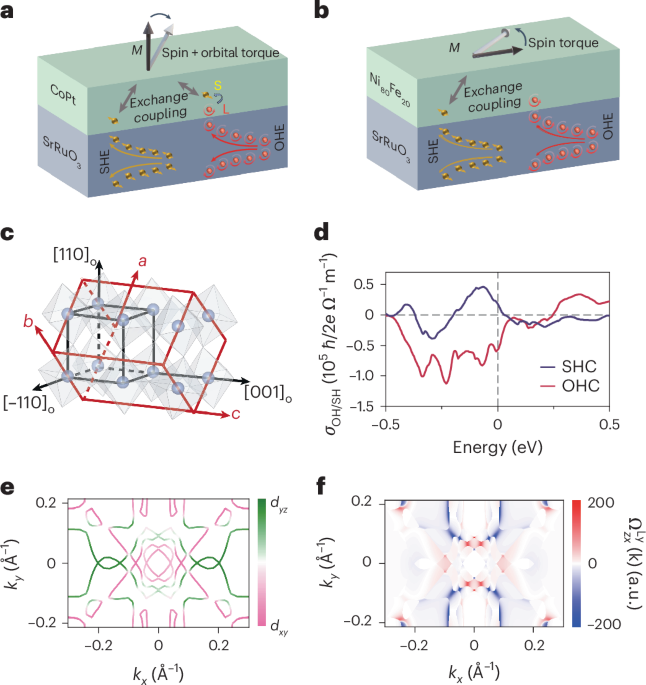
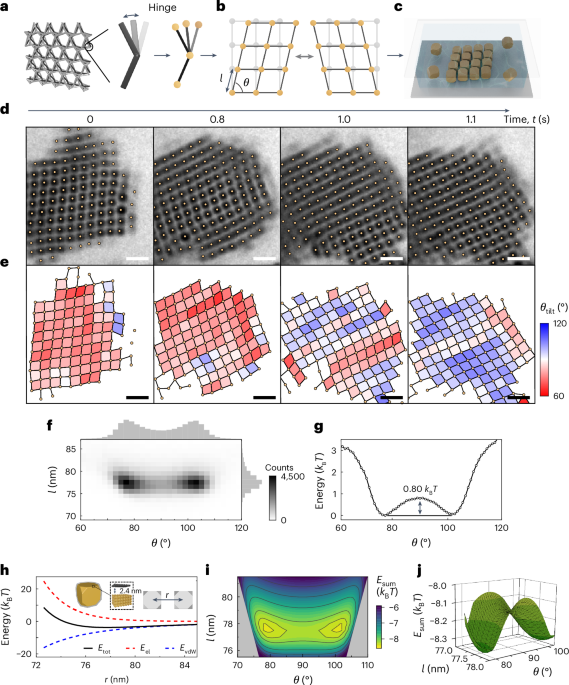
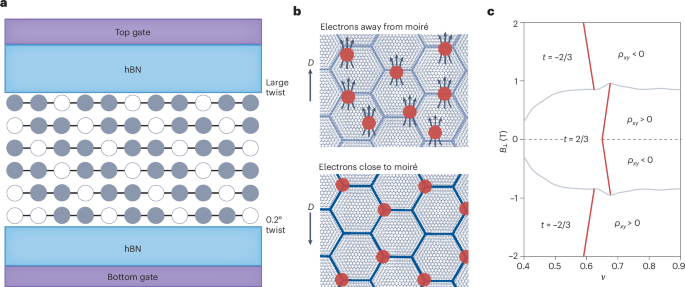
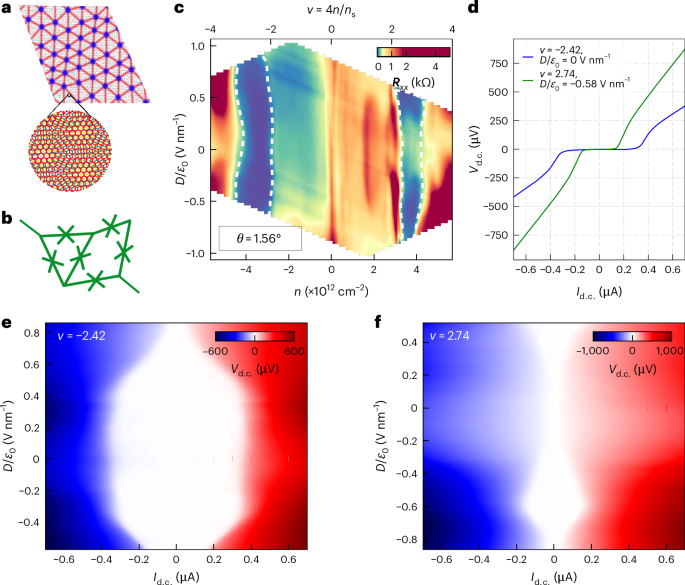
Most recently, the fractional quantum anomalous Hall effect (FQAHE) has been observed in several moiré systems, guided by theoretical predictions and by taking advantage of the twist degree of freedom. The challenging magnetotransport measurements in twisted MoTe2 were made possible by the fabrication of high-quality metal contacts on semiconductors, while the fabrication of a rhombohedral pentalayer graphene/hexagonal boron nitride moiré superlattice enabled the observation of the FQAHE in this system5,6,7. In this issue of Nature Materials, we highlight an Article from Xiaobo Lu, Jianpeng Liu and collaborators that expands the range of moiré materials exhibiting the FQAHE. They fabricated moiré superlattices consisting of rhombohedral hexalayer graphene and hexagonal boron nitride and performed magnetotransport measurements that establish both integer and fractional quantum anomalous Hall effects in this material. They further demonstrate that the FQAHE is tunable by both electric and magnetic fields, with the precise nature of these phase transitions being an open question. In the accompanying News & Views article, Yihang Zeng discusses how an advantage of this FQAHE material is that the required electric displacement field is lower and thus makes the system more resilient to dielectric breakdown and more accessible experimentally. The author also emphasizes that quasiparticles present in these fractional Chern insulators (which host the FQAHE) are strong candidates for implementation into topological quantum computation, but also highlights the many challenges including material quality, the vast parameter space and the need for theoretical guidance. However, Zeng also emphasizes that the FQAHE does not require a large external magnetic field and thus is accessible to a wide variety of experimental probes.
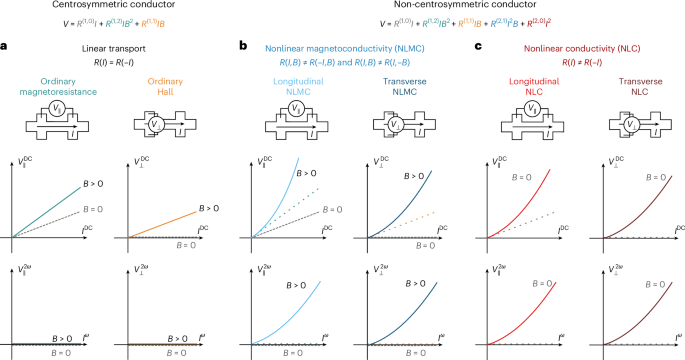
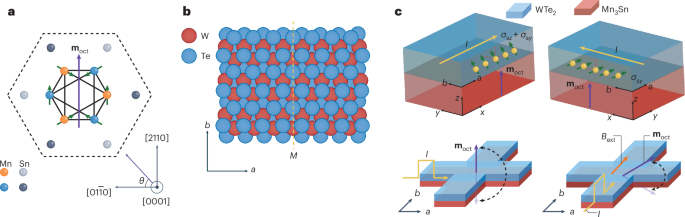
Nonlinear transport, where voltage is no longer directly proportional to current, has seen rapid advances in the past five years, in particular as a probe of the quantum properties of solids. In a Review Article on this topic, Luis Hueso and co-authors focus on second-order nonlinear effects, with quadratic scaling between voltage and current. Hueso and co-authors outline how, in the low-symmetry and nonlinear regimes, Hall responses and transverse voltages are not equivalent, providing helpful guidance on nomenclature for the community. Much work on nonlinear Hall responses was motivated by the discovery of a nonlinear anomalous Hall effect in non-magnetic WTe2 (refs. 8,9), which does not break time-reversal symmetry. The authors discuss the symmetry requirements to observe nonlinear responses and the wide variety of mechanisms responsible for such responses.
These works provide only a flavour for the vast observations of Hall effects in materials. Open questions remain for both the fundamental mechanisms and applications of many of these Hall effects, and we expect much fruitful research on these areas in the future.