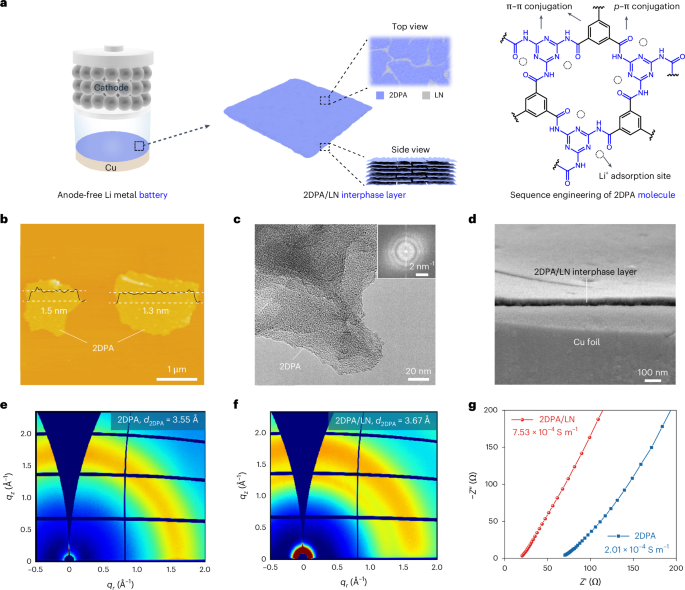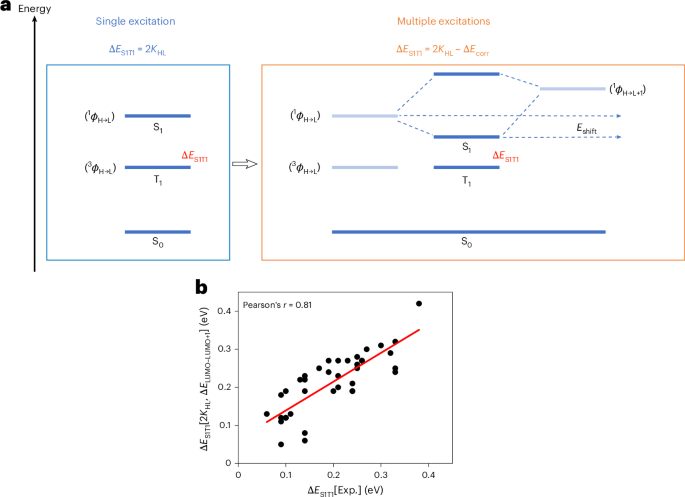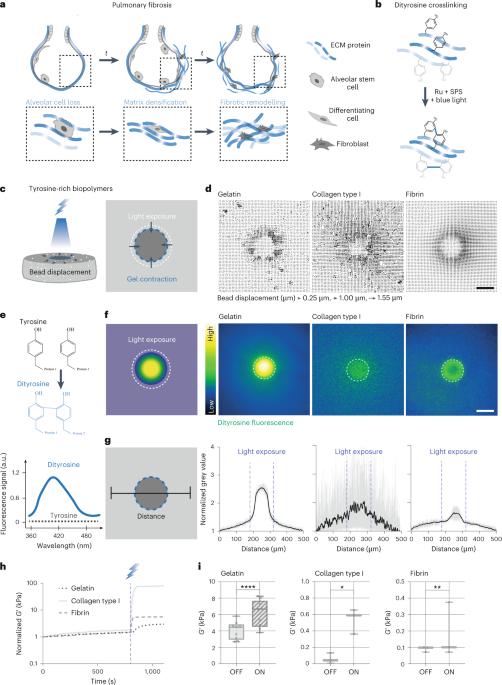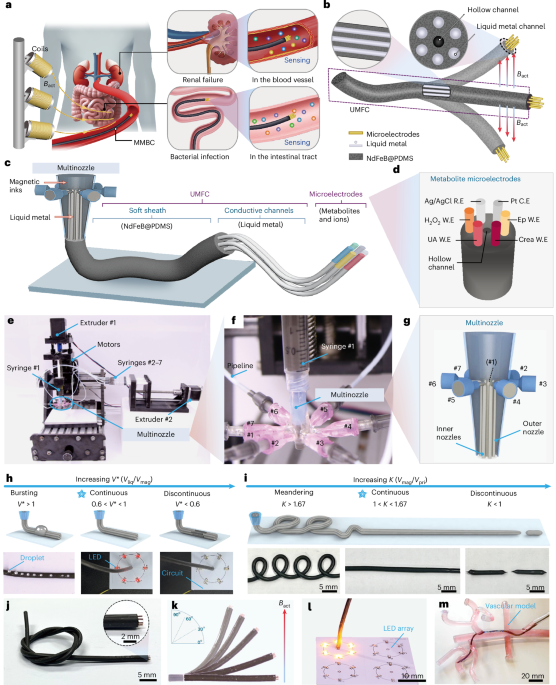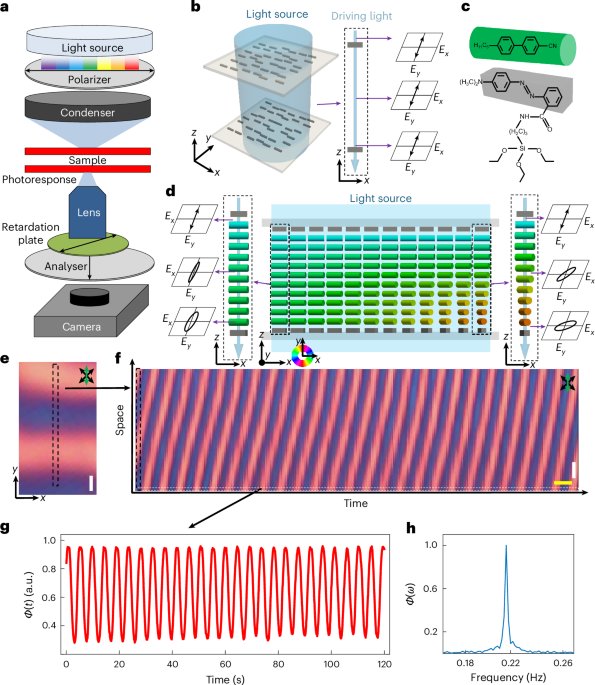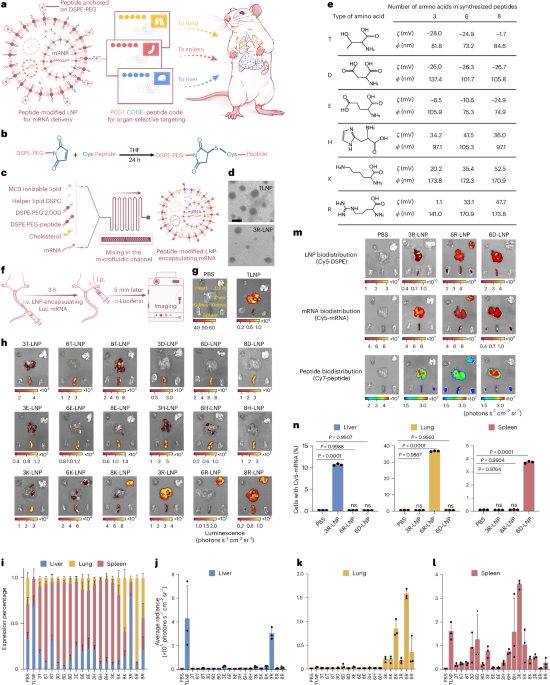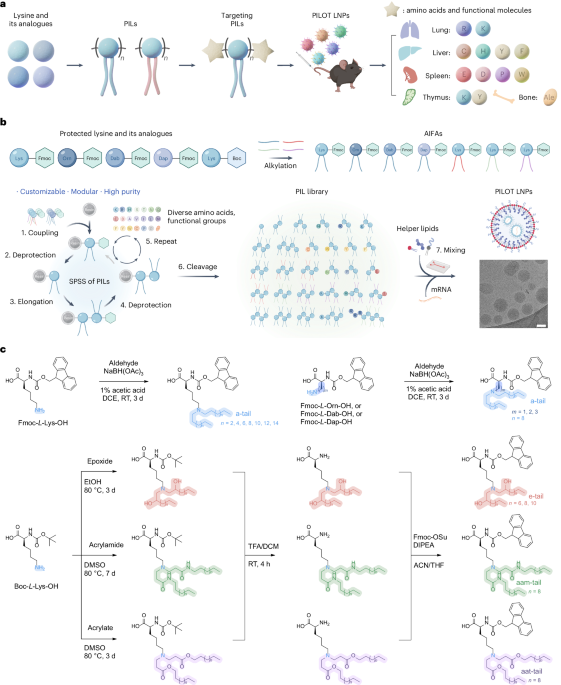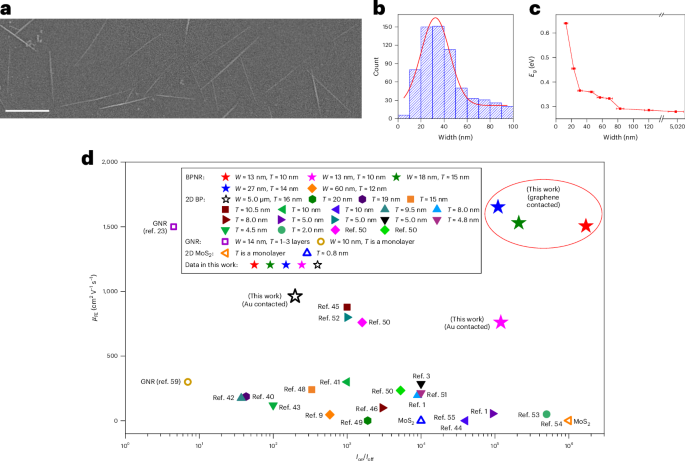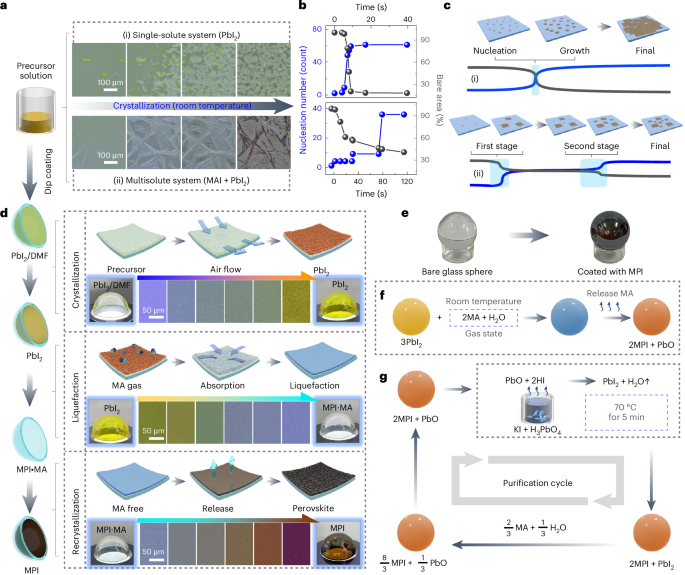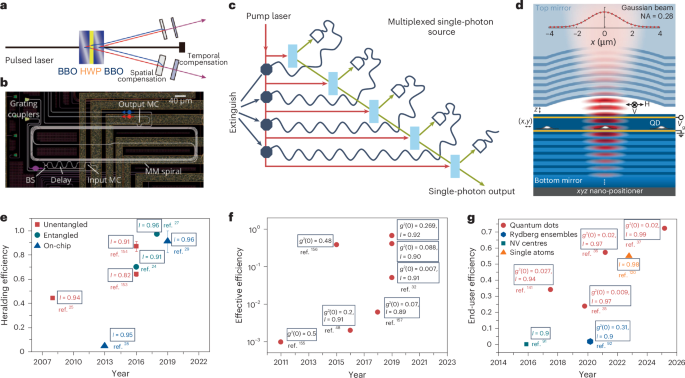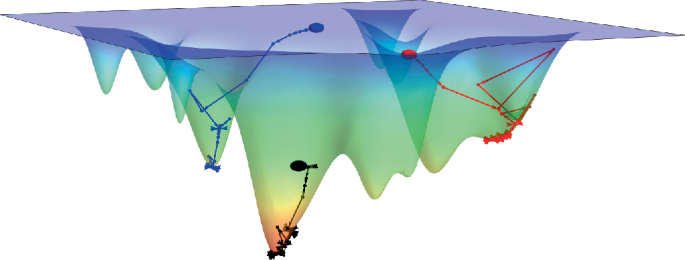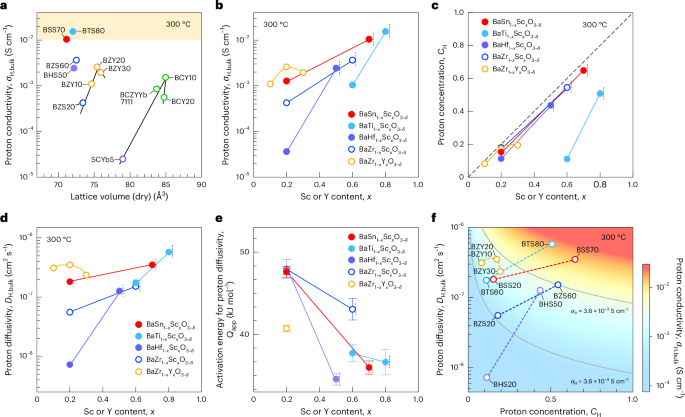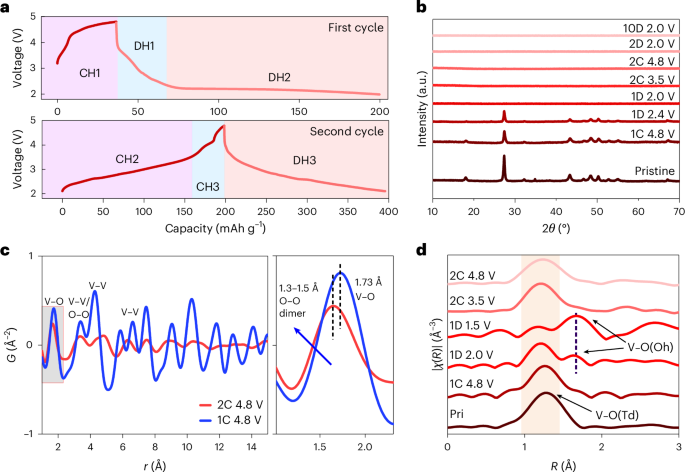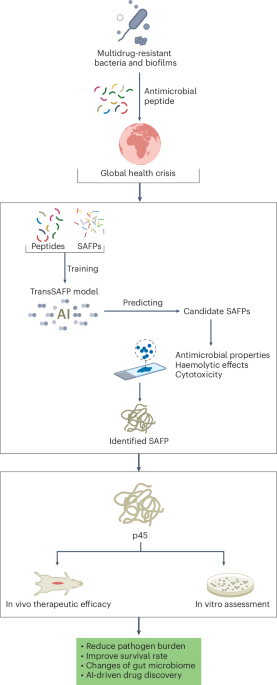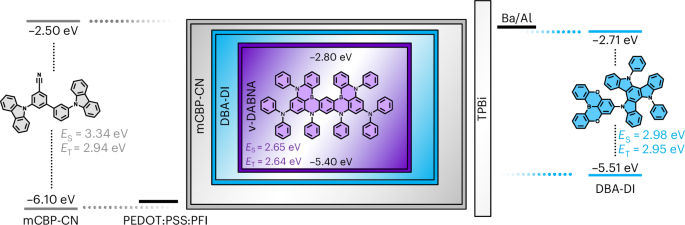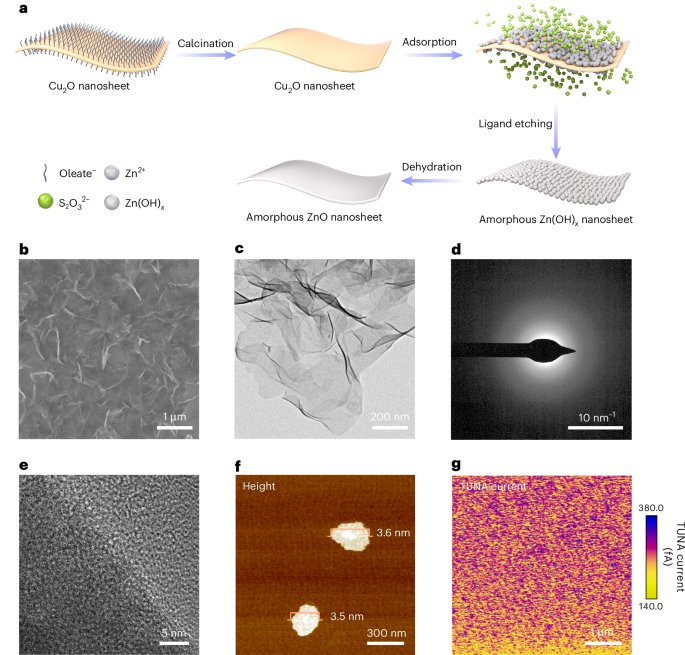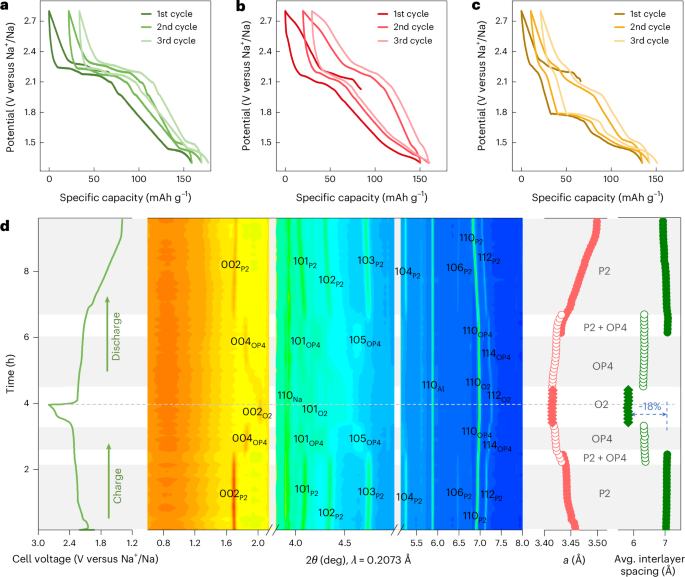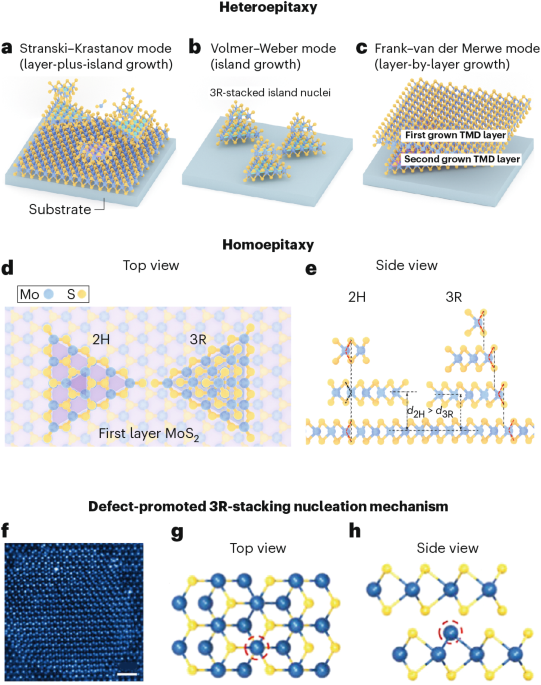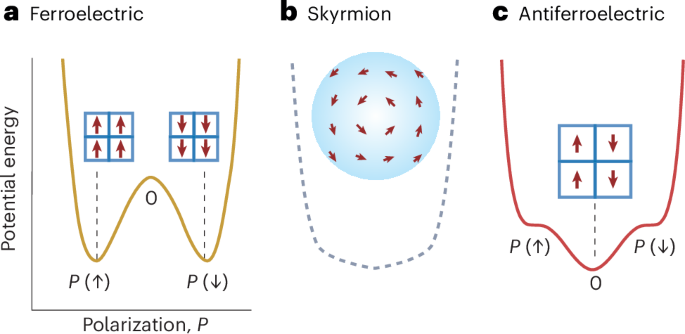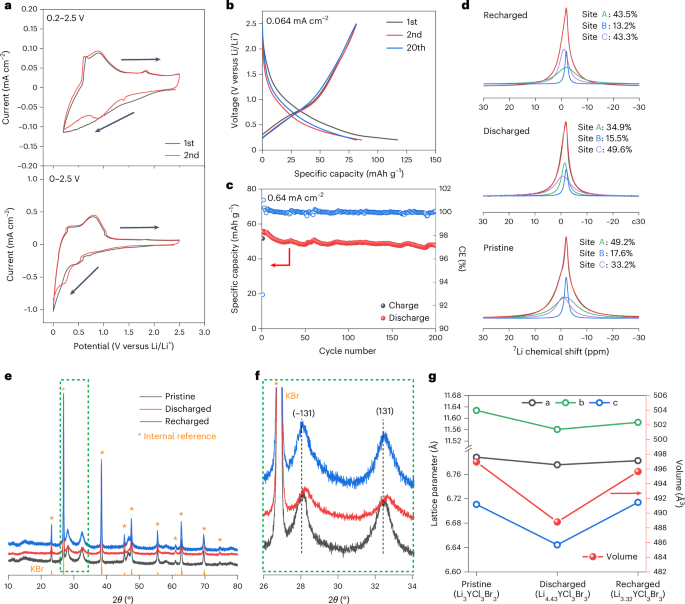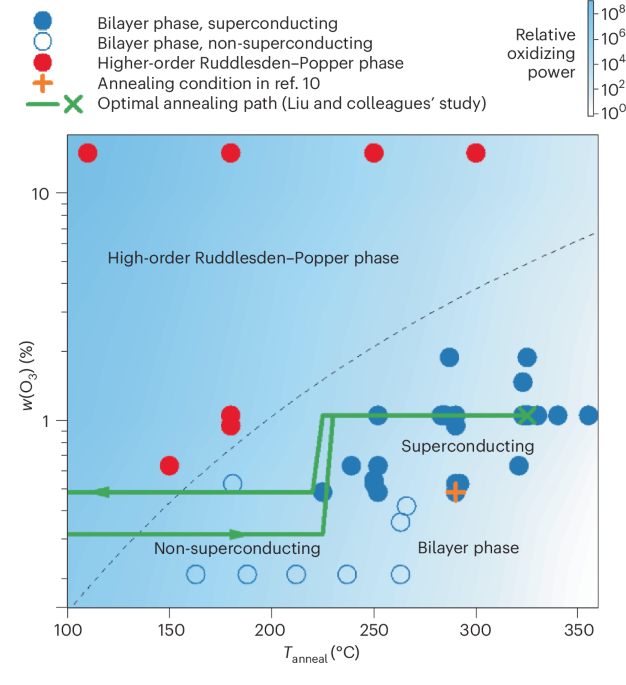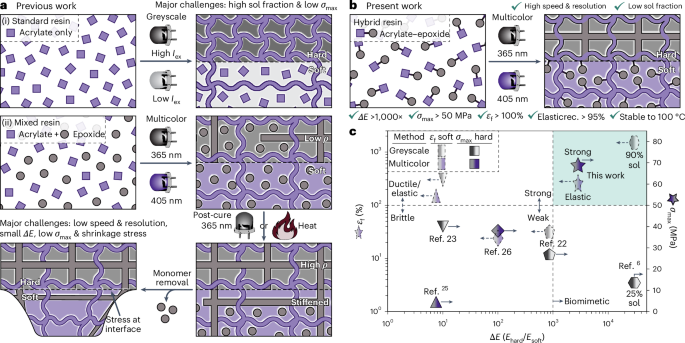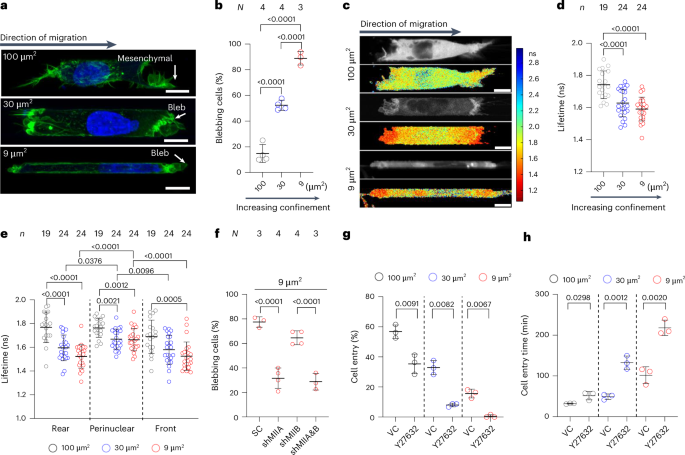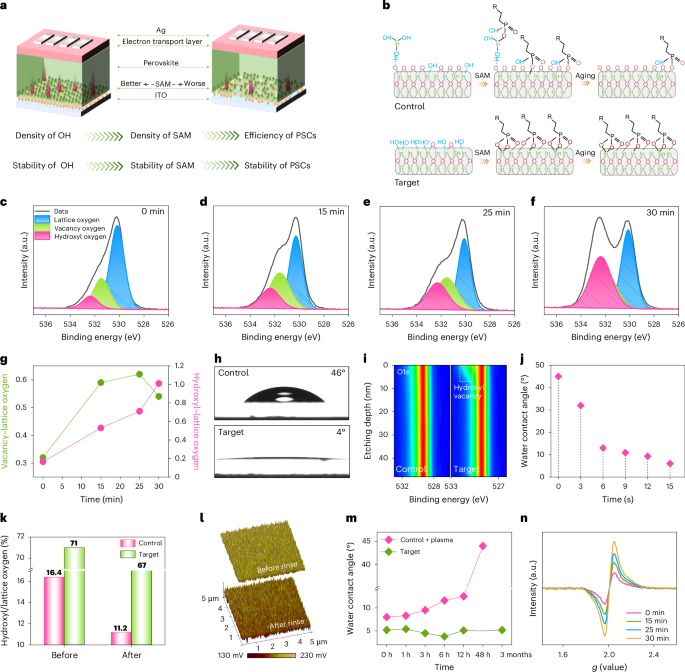
Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).
Google Scholar
Price, H. et al. Roadmap on topological photonics. J. Phys. Photonics 4, 032501 (2022).
Google Scholar
Bandres, M. A. et al. Topological insulator laser: experiments. Science 359, eaar4005 (2018).
Google Scholar
Contractor, R. et al. Scalable single-mode surface-emitting laser via open-Dirac singularities. Nature 608, 692–698 (2022).
Google Scholar
Kumar, A. et al. Topological sensor on a silicon chip. Appl. Phys. Lett. 121, 011101 (2022).
Blanco-Redondo, A., Bell, B., Oren, D., Eggleton, B. J. & Segev, M. Topological protection of biphoton states. Science 362, 568–571 (2018).
Google Scholar
Mittal, S., Goldschmidt, E. A. & Hafezi, M. A topological source of quantum light. Nature 561, 502–506 (2018).
Google Scholar
Dai, T. et al. Topologically protected quantum entanglement emitters. Nat. Photonics 16, 248–257 (2022).
Google Scholar
Hashemi, A., Zakeri, M. J., Jung, P. S. & Blanco-Redondo, A. Topological quantum photonics. APL Photonics 10, 010903 (2025).
Google Scholar
Nasari, H., Pyrialakos, G. G., Christodoulides, D. N. & Khajavikhan, M. Non-Hermitian topological photonics. Opt. Mater. Express 13, 870–885 (2023).
Google Scholar
Yan, Q. et al. Advances and applications on non-Hermitian topological photonics. Nanophotonics 12, 2247–2271 (2023).
Google Scholar
Kawabata, K., Shiozaki, K., Ueda, M. & Sato, M. Symmetry and topology in non-Hermitian physics. Phys. Rev. X 9, 041015 (2019).
Google Scholar
Meng, H., Ang, Y. S. and Lee, C. H. Exceptional points in non-Hermitian systems: applications and recent developments. Appl. Phys. Lett. 124, 060502 (2024).
Ding, K., Fang, C. & Ma, G. Non-hermitian topology and exceptional-point geometries. Nat. Rev. Phys. 4, 745–760 (2022).
Rudner, M. S. & Levitov, L. S. Topological transition in a non-Hermitian quantum walk. Phys. Rev. Lett. 102, 065703 (2009).
Google Scholar
Esaki, K., Sato, M., Hasebe, K. & Kohmoto, M. Edge states and topological phases in non-Hermitian systems. Phys. Rev. B 84, 205128 (2011).
Diehl, S., Rico, E., Baranov, M. A. & Zoller, P. Topology by dissipation in atomic quantum wires. Nat. Phys. 7, 971–977 (2011).
Google Scholar
Schomerus, H. Topologically protected midgap states in complex photonic lattices. Opt. Lett. 38, 1912–1914 (2013).
Google Scholar
Leykam, D., Bliokh, K. Y., Huang, C., Chong, Yi. Dong & Nori, F. Edge modes, degeneracies, and topological numbers in non-Hermitian systems. Phys. Rev. Lett. 118, 040401 (2017).
Google Scholar
Reséndiz-Vázquez, P., Tschernig, K., Perez-Leija, A., Busch, K. & León-Montiel, Roberto de J. Topological protection in non-HermitianHaldane honeycomb lattices. Phys. Rev. Res. 2, 013387 (2020).
Zeuner, J. M. et al. Observation of a topological transition in the bulk of a non-Hermitian system. Phys. Rev. Lett. 115, 040402 (2015).
Google Scholar
Weimann, S. et al. Topologically protected bound states in photonic parity–time-symmetric crystals. Nat. Mater. 16, 433–438 (2017).
Google Scholar
Zhao, H. et al. Non-Hermitian topological light steering. Science 365, 1163–1166 (2019).
Google Scholar
Liu, Y. G. N., Jung, P. S., Parto, M., Christodoulides, D. N. & Khajavikhan, M. Gain-induced topological response via tailored long-range interactions. Nat. Phys. 17, 704–709 (2021).
Weidemann, S., Kremer, M., Longhi, S. & Szameit, A. Topological triple phase transition in non-Hermitian Floquet quasicrystals. Nature 601, 354–359 (2022).
Google Scholar
Dai, T. et al. Non-Hermitian topological phase transitions controlled by nonlinearity. Nat. Phys. 20, 101–108 (2024).
Google Scholar
Bahari, B. et al. Nonreciprocal lasing in topological cavities of arbitrary geometries. Science 358, 636–640 (2017).
Google Scholar
St-Jean, P. et al. Lasing in topological edge states of a one-dimensional lattice. Nat. Photonics 11, 651–656 (2017).
Google Scholar
Zhao, H. et al. Topological hybrid silicon microlasers. Nat. Commun. 9, 981 (2018).
Google Scholar
Takata, K. & Notomi, M. Photonic topological insulating phase induced solely by gain and loss. Phys. Rev. Lett. 121, 213902 (2018).
Google Scholar
Zhu, B., Lang, Li-Jun, Wang, Q., Wang, Qi. Jie & Chong, Y. D. Topological transitions with an imaginary Aubry–André–Harper potential. Phys. Rev. Res. 5, 023044 (2023).
Google Scholar
Pereira, E. L., Li, H., Blanco-Redondo, A. & Lado, J. L. Non-Hermitian topology and criticality in photonic arrays with engineered losses. Phys. Rev. Res. 6, 023004 (2024).
Liu, S. et al. Gain- and loss-induced topological insulating phase in a non-Hermitian electrical circuit. Phys. Rev. Appl. 13, 014047 (2020).
Google Scholar
Gao, H. et al. Observation of topological edge states induced solely by non-Hermiticity in an acoustic crystal. Phys. Rev. B 101, 180303 (2020).
Google Scholar
Gao, H. et al. Non-Hermitian route to higher-order topology in an acoustic crystal. Nat. Commun. 12, 1888 (2021).
Google Scholar
Fan, H. et al. Hermitian and non-Hermitian topological edge states in one-dimensional perturbative elastic metamaterials. Mech. Syst. Signal Process. 169, 108774 (2022).
Wetter, H., Fleischhauer, M., Linden, S. & Schmitt, J. Observation of a topological edge state stabilized by dissipation. Phys. Rev. Lett. 131, 083801 (2023).
Google Scholar
On, M. B. et al. Programmable integrated photonics for topological Hamiltonians. Nat. Commun. 15, 629 (2024).
Dai, T. et al. A programmable topological photonic chip. Nat. Mater. 23, 928–936 (2024).
Google Scholar
Capmany, J. & Pérez-López, D. Programming topological photonics. Nat. Mater. 23, 874–875 (2024).
Cem, A., Sanchez-Jacome, D., Pérez-López, D. & Da Ros, F. Thermal crosstalk modeling and compensation for programmable photonic processors. In 2023 IEEE Photonics Conference, 1–2 (IEEE, 2023); https://doi.org/10.1109/IPC57732.2023.10360567
Aubry, S. & Andre, G. Analyticity breaking and anderson localization in incommensurate lattices. Ann. Isr. Phys. Soc. 3, 133 (1980).
Google Scholar
Verbin, M., Zilberberg, O., Lahini, Y., Kraus, Y. E. & Silberberg, Y. Topological pumping over a photonic Fibonacci quasicrystal. Phys. Rev. B 91, 064201 (2015).
Tambasco, Jean-Luc et al. Quantum interference of topological states of light. Sci. Adv. 4, eaat3187 (2018).
Google Scholar
Yuce, C. Pt symmetric Aubry–André model. Phys. Lett. A 378, 2024–2028 (2014).
Google Scholar
Longhi, S. Metal-insulator phase transition in a non-Hermitian Aubry–André–Harper model. Phys. Rev. B 100, 125157 (2019).
Google Scholar
Zeng, Q.-B., Yang, Y.-B. & Xu, Y. Topological phases in non-Hermitian Aubry–André–Harper models. Phys. Rev. B 101, 020201 (2020).
Pyrialakos, G. G. et al. Bimorphic Floquet topological insulators. Nat. Mater. 21, 634–639 (2022).
Google Scholar