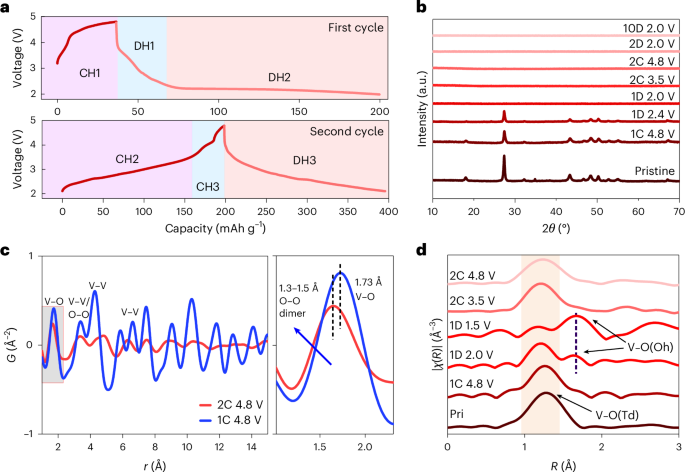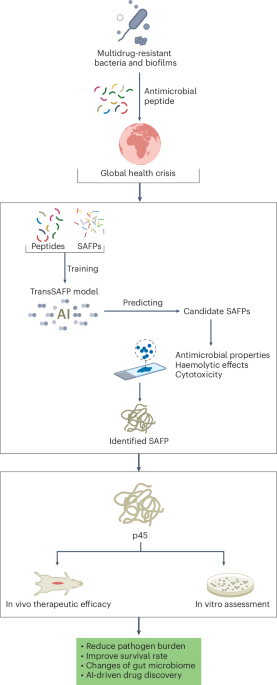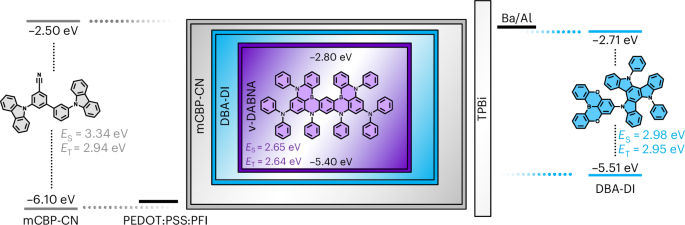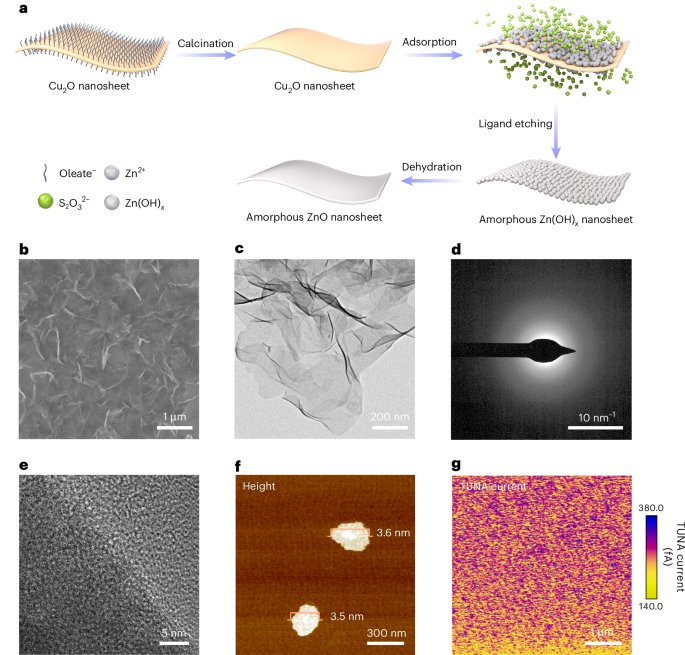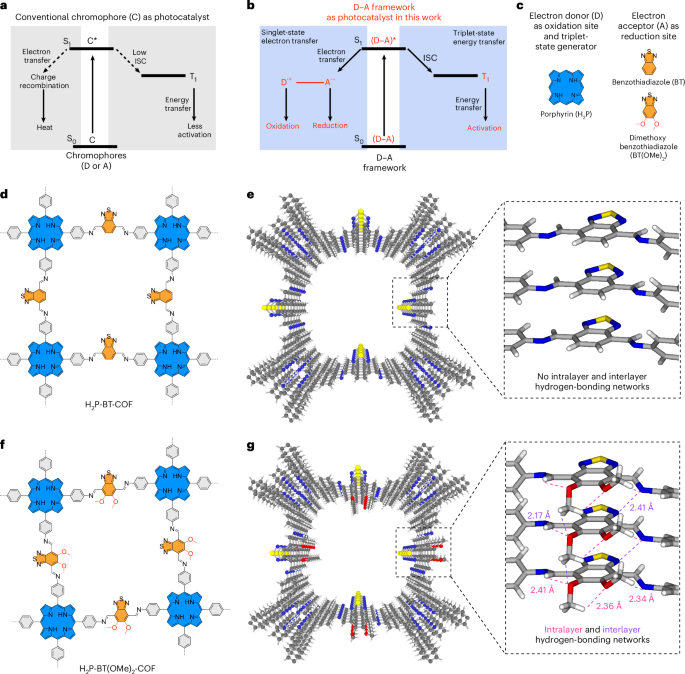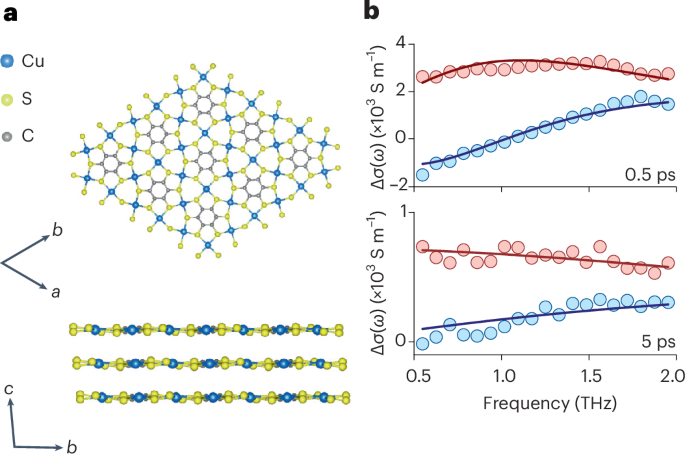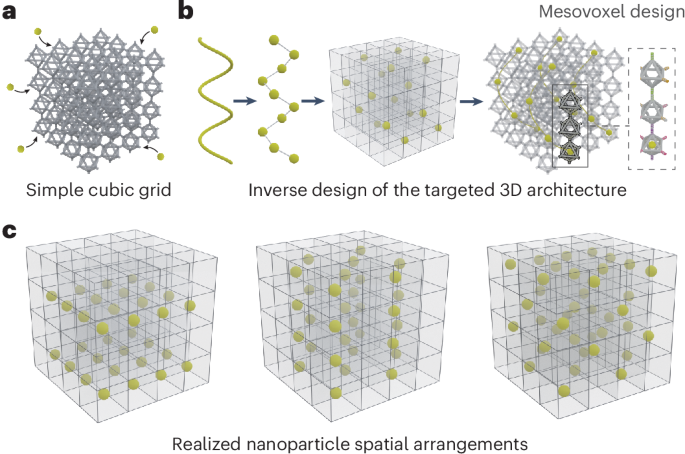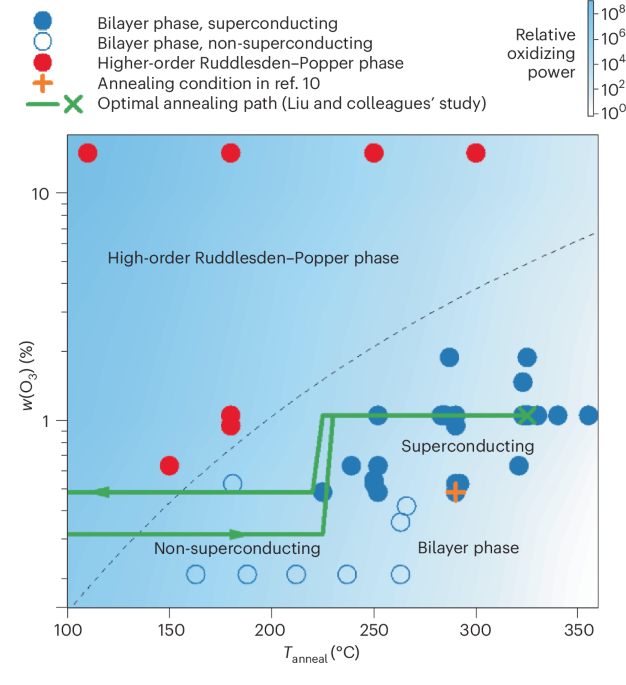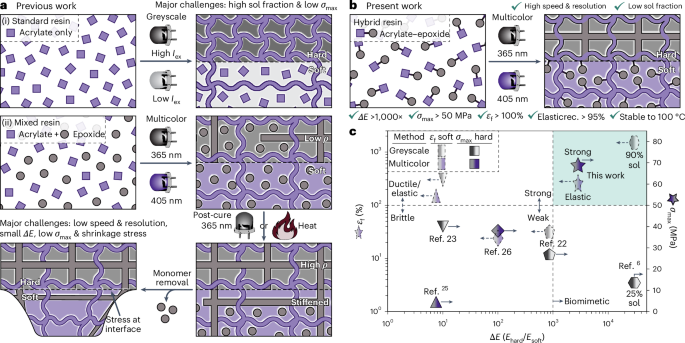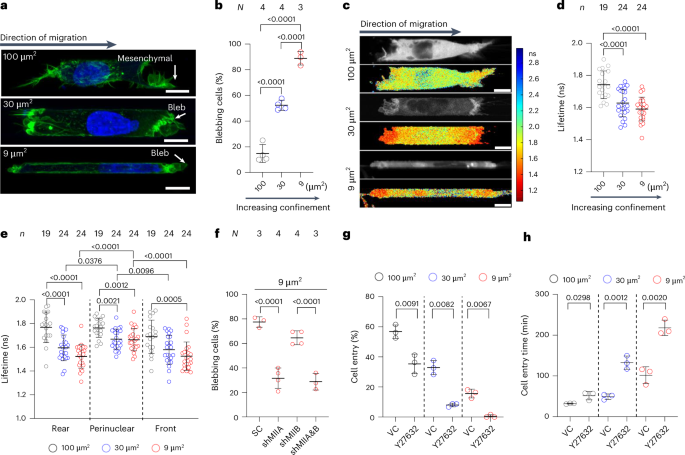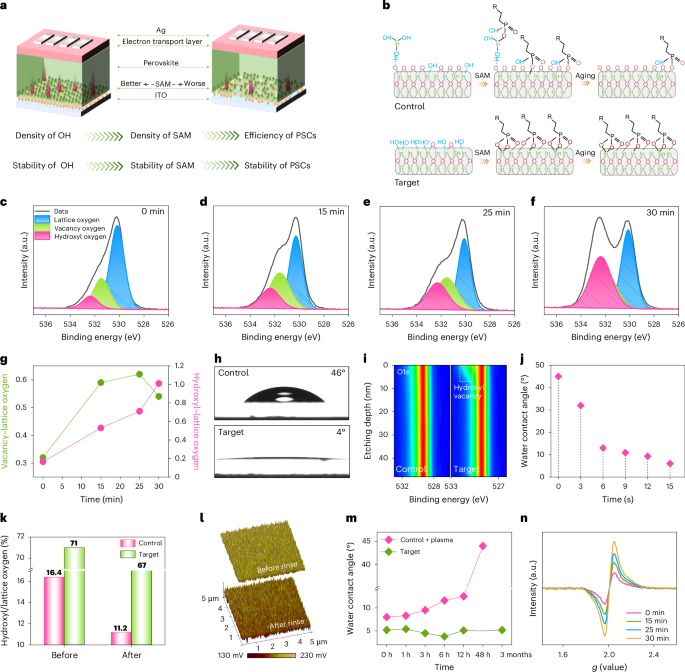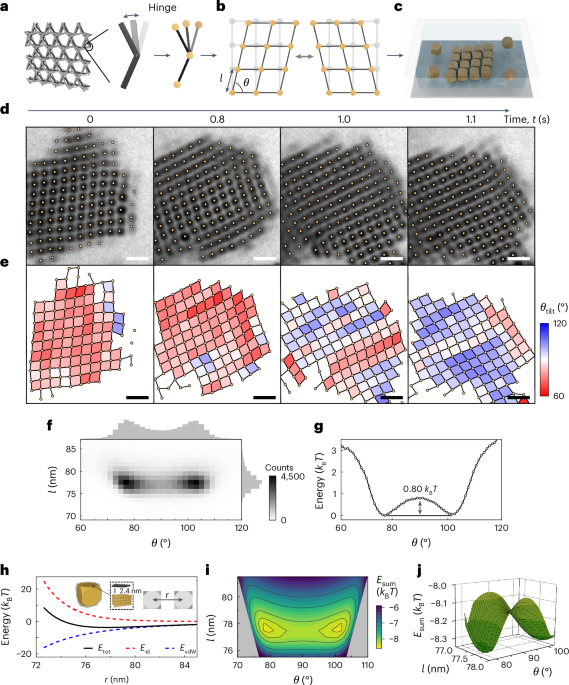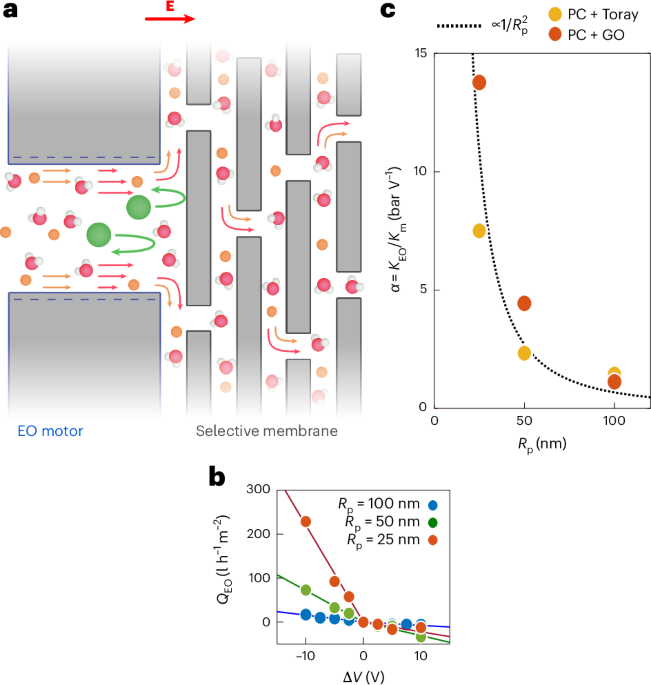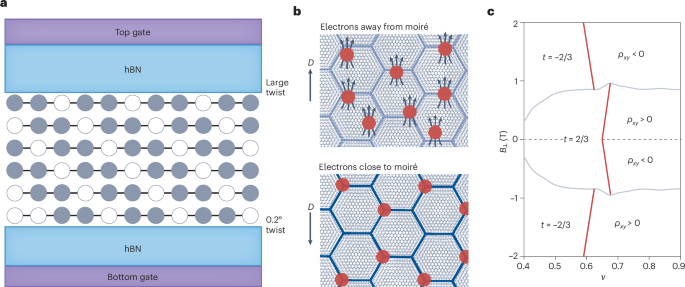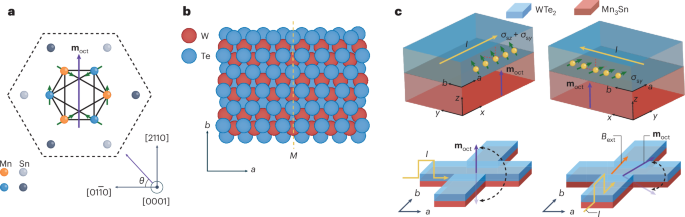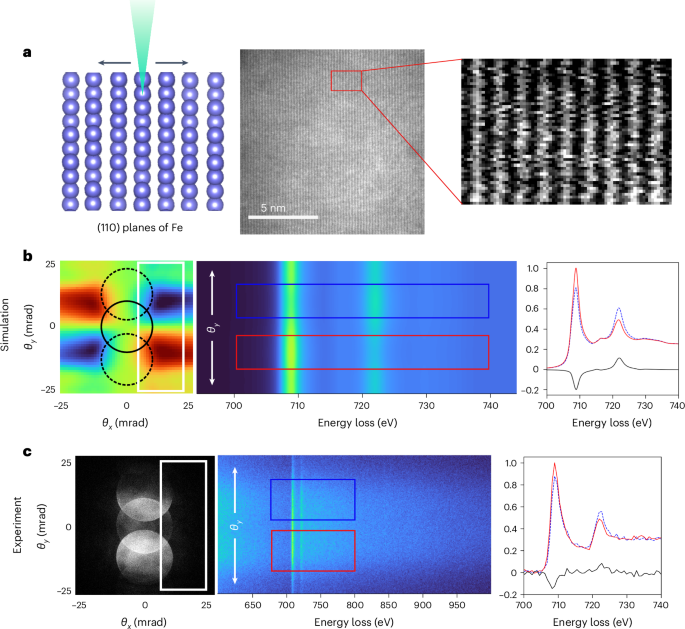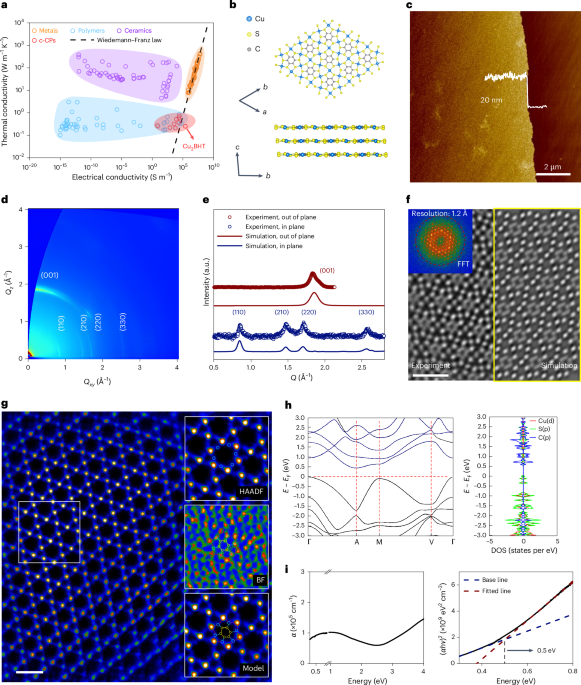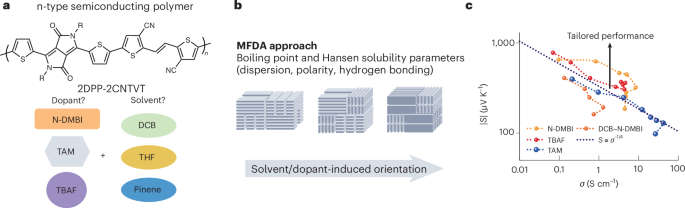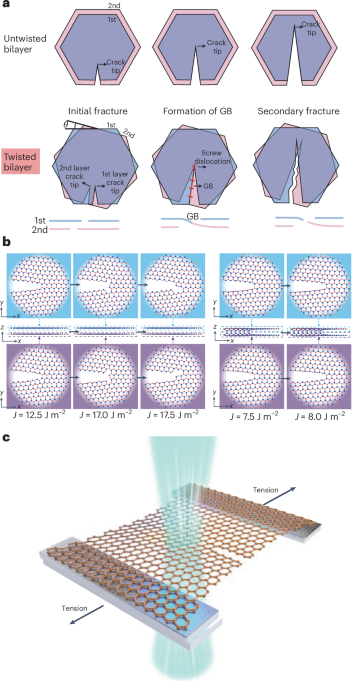
Chaikin, P. M. & Lubensky, T. C. Principles of Condensed Matter Physics (Cambridge Univ. Press, 2000).
Yeh, P. & Gu, C. Optics of Liquid Crystal Displays (Wiley, 2010).
Wilczek, F. Quantum time crystals. Phys. Rev. Lett. 109, 160401 (2012).
Google Scholar
Shapere, A. & Wilczek, F. Classical time crystals. Phys. Rev. Lett. 109, 160402 (2012).
Google Scholar
Wilczek, F. Superfluidity and space-time translation symmetry breaking. Phys. Rev. Lett. 111, 250402 (2013).
Google Scholar
Bruno, P. Impossibility of spontaneously rotating time crystals: a no-go theorem. Phys. Rev. Lett. 111, 070402 (2013).
Google Scholar
Watanabe, H. & Oshikawa, M. Absence of quantum time crystals. Phys. Rev. Lett. 114, 251603 (2015).
Google Scholar
Sacha, K. & Zakrzewski, J. Time crystals: a review. Rep. Prog. Phys. 81, 016401 (2017).
Yao, N. Y. & Nayak, C. Time crystals in periodically driven systems. Phys. Today 71, 40–47 (2018).
Khemani, V., Moessner, R. & Sondhi, S. L. A brief history of time crystals. Preprint at https://doi.org/10.48550/arXiv.1910.10745 (2019).
Sacha, K. Time Crystals (Springer International Publishing, 2020).
Guo, L. Phase Space Crystals: Condensed Matter in Dynamical Systems (IOP Publishing, 2021).
Zaletel, M. P. et al. Colloquium: quantum and classical discrete time crystals. Rev. Mod. Phys. 95, 031001 (2023).
Google Scholar
Sacha, K. Modeling spontaneous breaking of time-translation symmetry. Phys. Rev. A 91, 033617 (2015).
Khemani, V., Lazarides, A., Moessner, R. & Sondhi, S. L. Phase structure of driven quantum systems. Phys. Rev. Lett. 116, 250401 (2016).
Google Scholar
Else, D. V., Bauer, B. & Nayak, C. Floquet time crystals. Phys. Rev. Lett. 117, 090402 (2016).
Google Scholar
Yao, N. Y., Potter, A. C., Potirniche, I.-D. & Vishwanath, A. Discrete time crystals: rigidity, criticality, and realizations. Phys. Rev. Lett. 118, 030401 (2017).
Google Scholar
Zhang, J. et al. Observation of a discrete time crystal. Nature 543, 217–220 (2017).
Google Scholar
Choi, S. et al. Observation of discrete time-crystalline order in a disordered dipolar many-body system. Nature 543, 221–225 (2017).
Google Scholar
Smits, J., Liao, L., Stoof, H. T. C. & van der Straten, P. Observation of a space-time crystal in a superfluid quantum gas. Phys. Rev. Lett. 121, 185301 (2018).
Google Scholar
Liao, L., Smits, J., van der Straten, P. & Stoof, H. T. C. Dynamics of a space-time crystal in an atomic Bose-Einstein condensate. Phys. Rev. A 99, 013625 (2019).
Smits, J., Stoof, H. T. C. & van der Straten, P. Spontaneous breaking of a discrete time-translation symmetry. Phys. Rev. A 104, 023318 (2021).
Google Scholar
Randall, J. et al. Many-body–localized discrete time crystal with a programmable spin-based quantum simulator. Science 374, 1474–1478 (2021).
Google Scholar
Keßler, H. et al. Observation of a dissipative time crystal. Phys. Rev. Lett. 127, 043602 (2021).
Google Scholar
Taheri, H., Matsko, A. B., Maleki, L. & Sacha, K. All-optical dissipative discrete time crystals. Nat. Commun. 13, 848 (2022).
Google Scholar
Taheri, H., Matsko, A. B., Herr, T. & Sacha, K. Dissipative discrete time crystals in a pump-modulated Kerr microcavity. Commun. Phys. 5, 159 (2022).
Mi, X. et al. Time-crystalline eigenstate order on a quantum processor. Nature 601, 531–536 (2022).
Google Scholar
Frey, P. & Rachel, S. Realization of a discrete time crystal on 57 qubits of a quantum computer. Sci. Adv. 8, eabm7652 (2022).
Google Scholar
Kongkhambut, P. et al. Observation of a continuous time crystal. Science 377, 670–673 (2022).
Google Scholar
Liu, T., Ou, J.-Y., MacDonald, K. F. & Zheludev, N. I. Photonic metamaterial analogue of a continuous time crystal. Nat. Phys. 19, 986–991 (2023).
Google Scholar
Chen, Y.-H. & Zhang, X. Realization of an inherent time crystal in a dissipative many-body system. Nat. Commun. 14, 6161 (2023).
Google Scholar
Wu, X. et al. Dissipative time crystal in a strongly interacting Rydberg gas. Nat. Phys. 20, 1389–1394 (2024).
Google Scholar
Greilich, A. et al. Robust continuous time crystal in an electron–nuclear spin system. Nat. Phys. 20, 631–636 (2024).
Google Scholar
Carraro-Haddad, I. et al. Solid-state continuous time crystal in a polariton condensate with a built-in mechanical clock. Science 384, 995–1000 (2024).
Google Scholar
Yi, Y., Farrow, M. J., Korblova, E., Walba, D. M. & Furtak, T. E. High-sensitivity aminoazobenzene chemisorbed monolayers for photoalignment of liquid crystals. Langmuir 25, 997–1003 (2009).
Google Scholar
Landau, L. D. & Lifshitz, E. M. Statistical Physics (Elsevier, 2013).
de Gennes, P. G. & Prost, J. The Physics of Liquid Crystals (Clarendon Press, 1993).
Reichhardt, C., Reichhardt, C. J. O. & Milošević, M. V. Statics and dynamics of skyrmions interacting with disorder and nanostructures. Rev. Mod. Phys. 94, 035005 (2022).
Google Scholar
Smalyukh, I. I. Review: knots and other new topological effects in liquid crystals and colloids. Rep. Prog. Phys. 83, 106601 (2020).
Google Scholar
Zhao, H., Tai, J.-S. B., Wu, J.-S. & Smalyukh, I. I. Liquid crystal defect structures with Möbius strip topology. Nat. Phys. 19, 451–459 (2023).
Google Scholar
Mundoor, H., Senyuk, B. & Smalyukh, I. I. Triclinic nematic colloidal crystals from competing elastic and electrostatic interactions. Science 352, 69–73 (2016).
Google Scholar
Xu, S. & Wu, C. Space-time crystal and space-time group. Phys. Rev. Lett. 120, 096401 (2018).
Google Scholar
Gallego-Gómez, F., del Monte, F. & Meerholz, K. Optical gain by a simple photoisomerization process. Nat. Mater. 7, 490–497 (2008).
Google Scholar
Brener, E. A. & Marchenko, V. I. Nonlinear theory of dislocations in smectic crystals: an exact solution. Phys. Rev. E 59, R4752–R4753 (1999).
Google Scholar
Sohn, H. R. O. & Smalyukh, I. I. Electrically powered motions of toron crystallites in chiral liquid crystals. Proc. Natl Acad. Sci. USA 117, 6437–6445 (2020).
Google Scholar
Prigogine, I. Time, structure, and fluctuations. Science 201, 777–785 (1978).
Google Scholar
Zhang, R. et al. Spatiotemporal control of liquid crystal structure and dynamics through activity patterning. Nat. Mater. 20, 875–882 (2021).
Google Scholar
Zhao, H., Malomed, B. A. & Smalyukh, I. I. Topological solitonic macromolecules. Nat. Commun. 14, 4581 (2023).
Google Scholar
Lee, Y.-H. et al. Recent progress in Pancharatnam–Berry phase optical elements and the applications for virtual/augmented realities. Opt. Data Process. Storage 3, 79–88 (2017).
Cohen, E. et al. Geometric phase from Aharonov–Bohm to Pancharatnam–Berry and beyond. Nat. Rev. Phys. 1, 437–449 (2019).
Lyubarov, M. et al. Amplified emission and lasing in photonic time crystals. Science 377, 425–428 (2022).
Google Scholar
Chang, T. et al. Cellulose nanocrystal chiral photonic micro-flakes for multilevel anti-counterfeiting and identification. Chem. Eng. J. 446, 136630 (2022).
Google Scholar
Huang, W. & Mow, W. H. PiCode: 2D barcode with embedded picture and ViCode: 3D barcode with embedded video. In Proc. 19th Annual International Conference on Mobile Computing & Networking 139–142 (ACM, 2013).
Chang, S. et al. Electrical tuning of branched flow of light. Nat. Commun. 15, 197 (2024).
Google Scholar
Poy, G. et al. Interaction and co-assembly of optical and topological solitons. Nat. Photon. 16, 454–461 (2022).
Google Scholar
Martinez, A., Mireles, H. C. & Smalyukh, I. I. Large-area optoelastic manipulation of colloidal particles in liquid crystals using photoresponsive molecular surface monolayers. Proc. Natl Acad. Sci. USA 108, 20891–20896 (2011).
Google Scholar
Lee, T., Trivedi, R. P. & Smalyukh, I. I. Multimodal nonlinear optical polarizing microscopy of long-range molecular order in liquid crystals. Opt. Lett. 35, 3447–3449 (2010).
Google Scholar