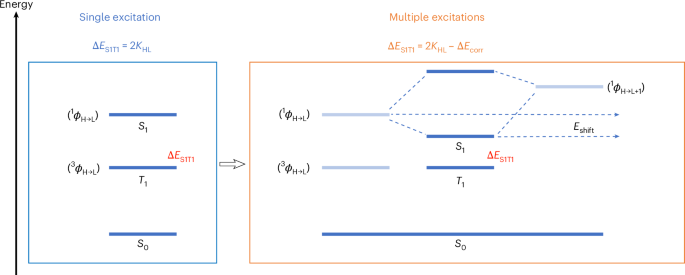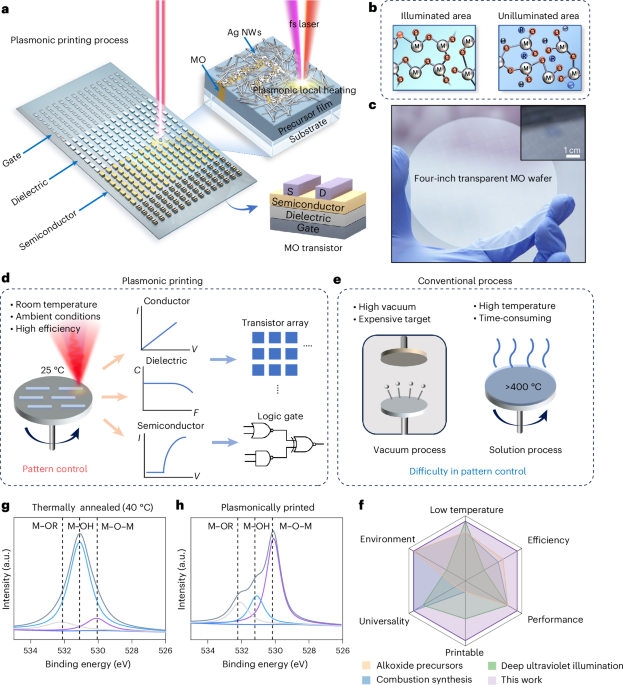
The family of twisted multilayer graphene devices, like twisted bilayer and trilayer graphene, provide an opportunity to study the origin of superconductivity (SC) in these materials hosting flatbands1,2,3. The magic-angle twisted trilayer graphene (MATTG) hosts both Dirac band and moiré flatband4,5, and exhibits Pauli-limit violation3,6. Such exotic properties make MATTG an interesting system to study. Recent microscopic theoretical studies show that the superconducting regions are surrounded in the phase diagram by phases and ordering of different kinds7,8,9,10, making spin (valley) configuration and spin (valley) fluctuations an important physics in the system. The co-existence of different phases may give rise to competition between them11.
The stacking of atomically thin sheets of graphene with a twist angle gives rise to lattice reconstruction and lattice relaxation effects. In general, moiré systems can also incur moiré of moiré superstructure domains due to strong lattice relaxation12. Studies using scanning tunnelling microscopy techniques have revealed the presence of quasi-one-dimensional ‘moiré solitons’ and point-like faults called ‘twistons’ in MATTG13,14 due to moiré lattice reconstruction. The presence of such relaxation-induced moiré inhomogeneities distinct from twist-angle disorder can make the understanding of underlying mechanisms more challenging. Intrinsic mesoscopic inhomogeneities also exist in systems like LaAlO3/SrTiO3 (LAO/STO)15,16 exhibiting a broadened Berezinskii–Kosterlitz–Thouless (BKT) transition17,18. The measurement of superfluid stiffness using BKT-like analysis is a route to extract important information about SC in MATTG and moiré inhomogeneity makes it challenging.
In this Article, we report evidence of competing order and moiré inhomogeneity in the superconducting phase of MATTG, through quantum transport and switching measurements in the superconducting and neighbouring normal states. We present the switching measurements as a new approach to understand these superconductors. They are studied with both temperature and in-plane magnetic fields to understand the system’s spin configuration and ground state. We report a non-monotonic behaviour of the switching distributions with temperature strongly pointing towards a competing order, probably magnetic in origin, in the ground state. The switching measurement is largely successful in bringing out exciting features in the system as the mesoscopic moiré inhomogeneity in the system allows us to describe it as an array of Josephson junctions (JJs). The switching distribution points towards evidence of a magnetic order when probed with an in-plane magnetic field. The observation of hysteresis, in the proximal normal phase, in magnetoresistance with an in-plane magnetic field provides direct evidence to support the results of switching measurements. Our experiments and analysis also provide a way to infer the difficult-to-measure quantity of superfluid stiffness—an estimate in the MATTG system; this reveals that the observation of BKT transition in the system is broadened due to moiré inhomogeneity.
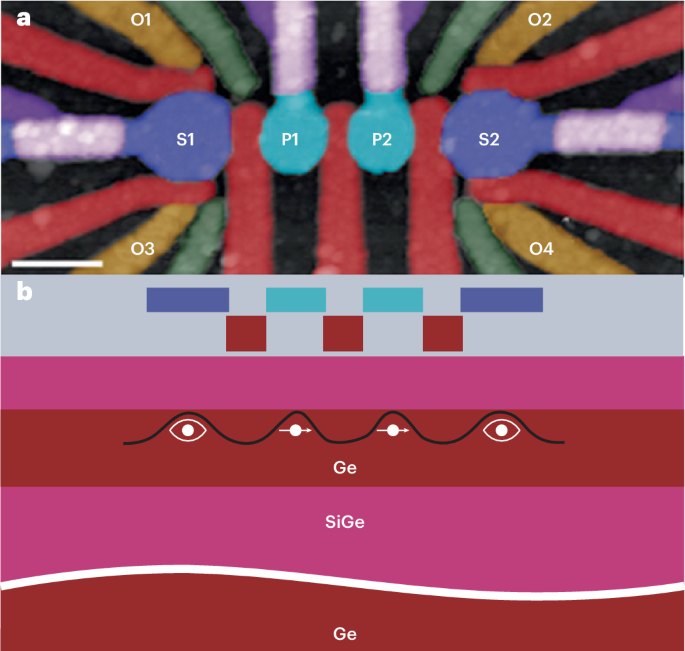
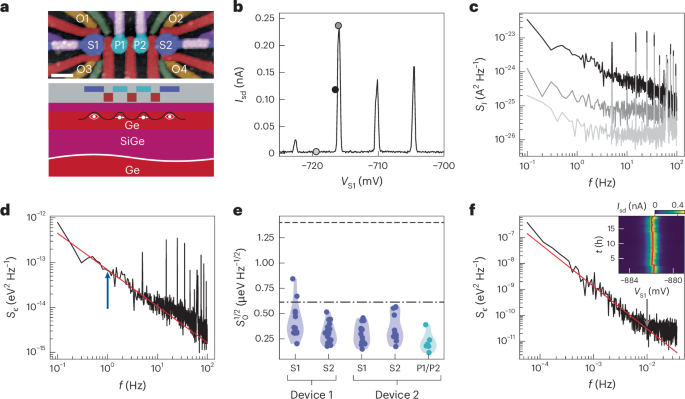
MATTG is a mirror-symmetric stacking of three layers of graphene—with the middle layer twisted by the magic angle (Supplementary Section II shows different twist angles realized in devices). The stack is encapsulated in hexagonal boron nitride and has a top gate and bottom gate. The dual-gate geometry allows independent control over charge density n and applied perpendicular electric displacement field D (Supplementary Sections III and IV show the fabrication and measurement details, respectively).
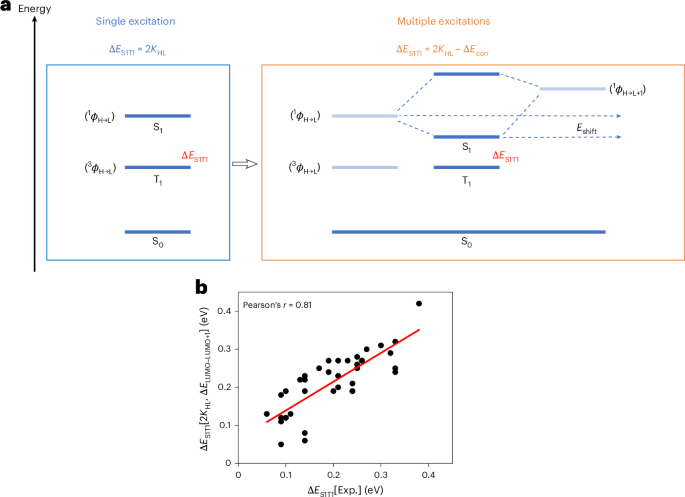
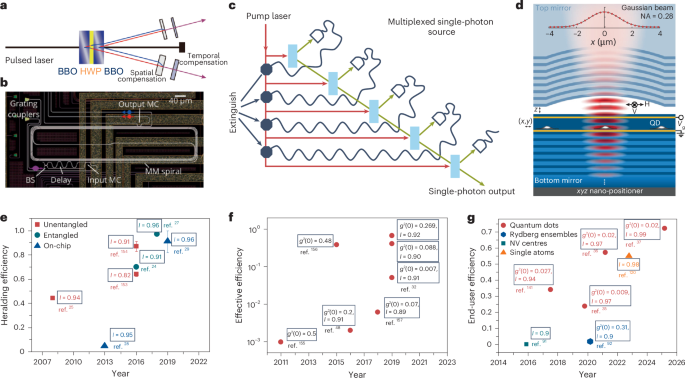
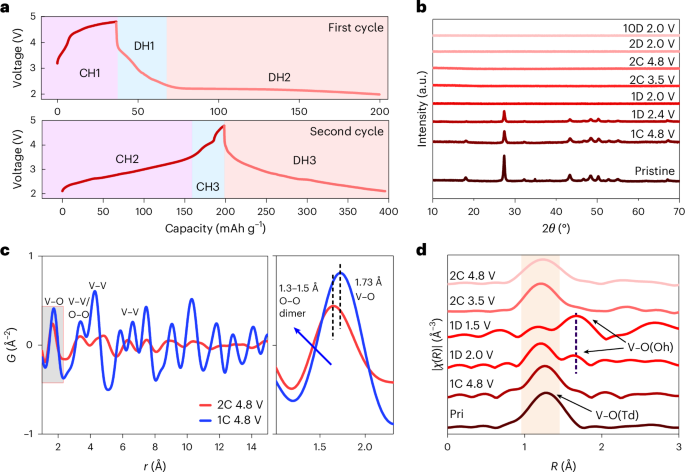
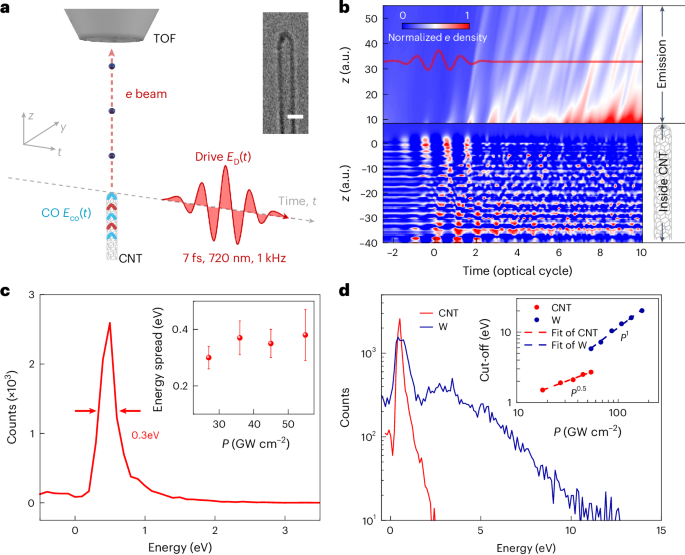
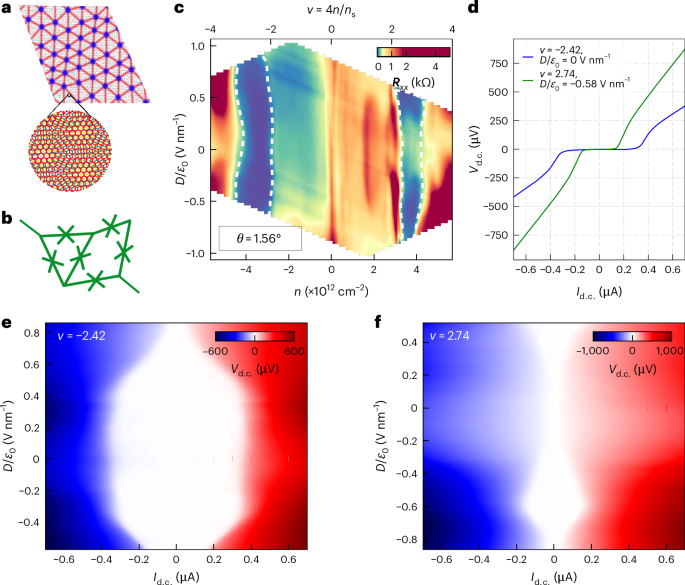
MATTG has been reported as a robust superconductor having a critical temperature of Tc ≈ 2 K with predictions of exotic superconducting properties like spin-triplet SC6,8,19,20,21,22. Figure 1a shows a schematic of the formation and manifestation of twistons and moiré solitons in the MATTG system. The plaquette regions have a twist angle that is close to the magic angle of 1.56°, whereas the twiston and soliton regions have higher twist angles due to lattice relaxation13. Such twist-angle variations among the regions lead to different moiré length scales and, in turn, give rise to variations in the local filling factor. The twiston and soliton regions have smaller filling factors and, thus, act as weak links to the superconducting plaquettes (details of variation in the density of states with the local twist angle from non-interacting theory are provided in Supplementary Section I). Weak links distributed in the system lead to the formation of a network of JJs (Fig. 1b), which is discussed in detail later. We report that MATTG hosts SC in both hole-doped regime and electron-doped regime—consistent with past studies. The filling ν = 4n/ns, where ns = 5.67 × 1012 cm−2 is the superlattice density, and D/ϵ0 where the SC emerges, representing the zero longitudinal resistance Rxx, is around filling ν = ±3 (Fig. 1c). We note critical temperatures of around 1.6 K and 1.2 K in the hole- and electron-doped regimes, respectively (Supplementary Section V). Figure 1d shows the d.c. Vd.c.–Id.c. curves at optimal hole and electron fillings. We find a critical current of around 400 nA for optimal hole biasing of ν = −2.42 and D/ϵ0 = 0 V nm–1 and 200 nA for optimal electron biasing of ν = 2.74 and D/ϵ0 = −0.58 V nm–1—comparable with other reported values in the literature1,2,19. We also measure other superconducting MATTG devices, one with a critical current of around 50 nA for optimal hole biasing and another with a critical current of around 380 nA in the hole-biased regime (Supplementary Section VI).
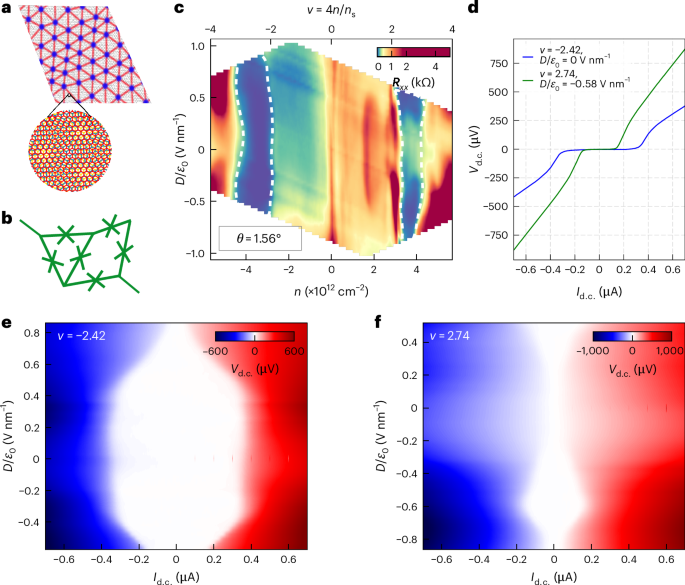
a, Schematic of the moiré lattice reconstruction, leading to the formation of an array of twistons (shaded in blue) and moiré solitons (shaded in red), featuring local twist-angle faults. Inset: a close-up perspective of the MATTG moiré, illustrating the contrasting length scales of solitons and moiré. b, In the superconducting state, moiré twistons and solitons in a twisted trilayer graphene serve as weak links within the superconductor, forming a network of JJs. c, Longitudinal resistance Rxx as a function of carrier density n, filling ν and electric field D/ϵ0 at T = 20 mK and B = 0 T. The superconducting regions have been marked by a white dashed outline. d, The d.c. voltage drop across the device as a function of d.c. current bias at optimal hole and electron doping. The hole-doped side and electron-doped side have a maximum critical current of ~400 nA and ~200 nA, respectively. e,f, The d.c. Vd.c.–Id.c. curves at the optimal hole (e) and electron (f) doping with varying D/ϵ0 values. The white part represents a zero voltage drop and the superconducting part before it turns normal (red/blue). The boundary of the white region gives us an idea about the critical current at a particular D/ϵ0 value.
Source data
The electric field D/ϵ0 can be tuned to study different phases in MATTG. Here we study the modulation of the strength of SC in the system with D/ϵ0. Figure 1e,f shows the Vd.c.–Id.c. curves as a function of D/ϵ0 for optimal hole and electron filling, respectively. The hole-side superconducting phase is the strongest at zero electric field and weakens after an electric field of ±0.50 V nm–1. By contrast, the electron-side superconducting phase hosts the maximum critical current at a finite electric field of 0.59 V nm–1 and is considerably weaker at 0 V nm–1 (Supplementary Section VII provides further device characterization). Our observation of the distinct dependence of SC on the electric field in electron and hole fillings is consistent with past experiments7,8,9. We next discuss a method of studying SC that has not been used for twistronic superconductors.
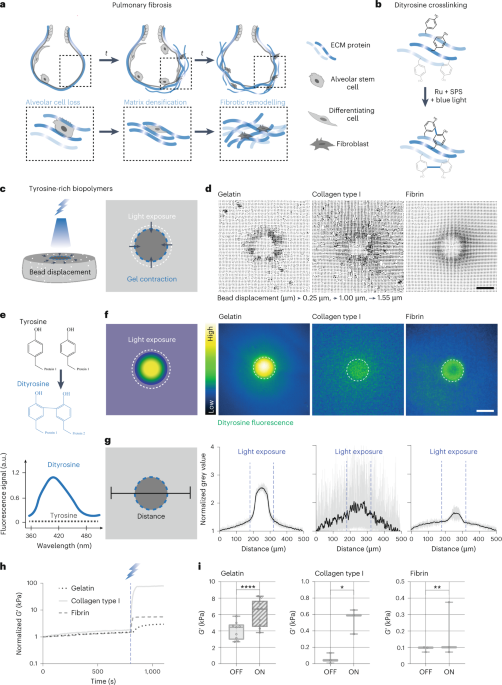
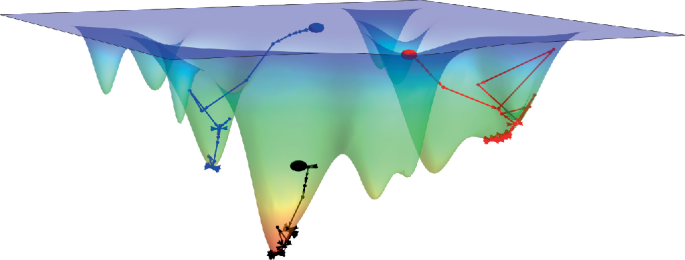
The switching measurements capturing the transition from a superconducting to a dissipative state bring out the stochastic nature of the switching current Is—one that is not apparent in a single Vd.c.–Id.c. measurement. The switching of JJs, being a stochastic process, leads to the switching taking place at different bias currents (Fig. 2a). Figure 2b shows a schematic of the washboard potential landscape associated with the resistively and capacitively shunted junction model that captures the dynamics of a JJ. On increasing the current bias, the potential tilts, and the particle in the landscape can escape the potential barrier. The escape is analogous to the JJ switching from the superconducting state to the normal state. The stochastic nature of the switching of JJs is captured in the histogram of the switching current (Fig. 2b, inset). When the bias current is low, the likelihood of transitioning into the running state is lower compared with when the potential becomes more tilted, resulting in a shallower potential well at higher bias currents. The counts at the lower bias currents are smaller than the higher bias currents, giving rise to the long tail at the lower currents and asymmetric or skewed shape of the switching histograms observed in numerous previous studies23,24,25,26. Our observation of similarly skewed histograms provides evidence against the influence of noise in our measurements. Each histogram showcases large statistics that help provide insights into the nature of the superconducting transition, inhomogeneities in the system and energetics25,26. We record 10,000 switching events to gather a normalized histogram distribution of Is. Figure 2c presents the principle of the switching current measurement technique, which allows us to gather large statistics about the stochastic quantity of Is (Supplementary Section VIII provides details of the switching measurements).
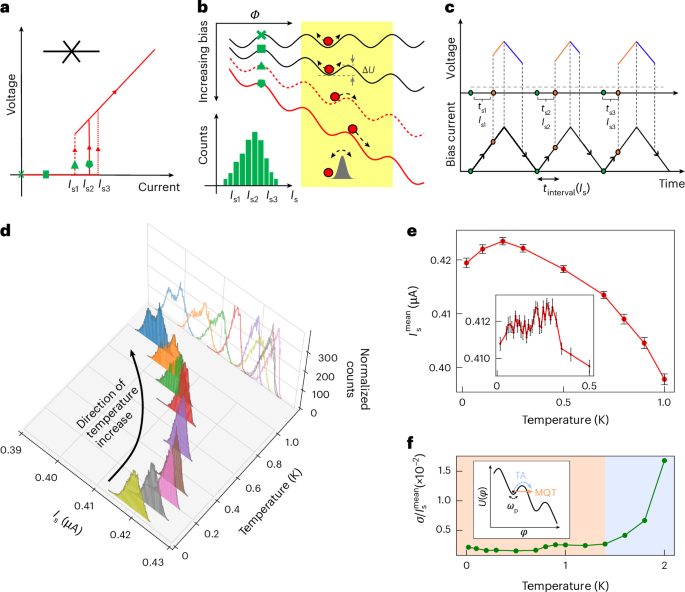
a, The Vd.c.–Id.c. characteristics of a JJ showing the different switching currents. b, The tilted washboard potential captures the JJ switching from the superconducting state to the normal state by an analogous picture of a particle crossing the potential barrier ΔU. Larger current biases (identified by symbols in a) tilt the washboard potential more, making it easier for the particle to cross the now-tilted barrier. Inset: the switching histogram showcases the stochastic nature of the JJ switching at different switching currents. c, To gather statistics of the switching current, a low-frequency triangular wave is applied by a function generator. The current varies linearly with time, starting from zero and reaching a value slightly above the critical current. The counter measures the elapsed time (ts) from the onset of zero-bias current (green dot) to the instance of transition from the superconducting state to the normal state (red dot). The ts value determines Is, considering the frequency and amplitude of the triangular signal. d, Switching histograms at the optimal hole-side doping and electric field (ν, D/ϵ0) = (–2.42, 0) as a function of temperature. The distributions evolve non-monotonically with temperature. The arrow represents the direction of temperature sweep. e, Mean current of the switching distributions \({I}_{{\rm{s}}}^{{\rm{mean}}}\) plotted as a function of temperature shows a non-monotonic behaviour. Inset: \({I}_{s}^{{\rm{mean}}}\) plotted with a temperature bin of 10 mK clearly shows the non-monotonic behaviour at (ν, D/ϵ0) = (–2.42, –0.29). The error bars denote the standard deviations of individual distributions of 10,000 data points each. f, Standard deviation normalized by the mean of the distributions \(\sigma /{I}_{{\rm{s}}}^{{\rm{mean}}}\) plotted as a function of temperature. The trend of the evolution of \(\sigma /{I}_{{\rm{s}}}^{{\rm{mean}}}\) with temperature denotes the different switching processes dominating at different temperatures. The initial temperature-independent MQT process (orange shading) transitions into the TA process (blue shading), where \(\sigma /{I}_{{\rm{s}}}^{{\rm{mean}}}\) increases. Inset: the washboard potential U varies as a function of phase Φ. The different switching processes—TA and MQT—are shown schematically, where ωp is the frequency of oscillation of the particle in the potential well.
Source data
Figure 2d shows the switching distributions, as a function of temperature, at the optimal hole filling. The mean switching current \({I}_{s}^{{\rm{mean}}}\) of the distribution has a non-monotonic behaviour—increases with temperature up to ~200 mK and decreases thereafter (Fig. 2e). This non-monotonic response is not expected for conventional JJs. A possible way for the increase in \({I}_{s}^{\;{\rm{mean}}}\) with temperature up to 200 mK is the suppression of a competing order to give way to the superconducting state—noted as an enhancement in the critical current7,8 (Supplementary Section IX shows a simple phenomenological model). A non-monotonic evolution of \({I}_{s}^{{\rm{mean}}}\) is also noted in the electron-doped SC (Supplementary Section X provides additional data). Such an enhancement in critical current has been reported previously for magnetic-ordered materials27, and materials having a d-wave superconducting order parameter28. This forms our motivation to look for a competing order that is magnetic in nature. Here we provide the first indication of the competing magnetic ground states in MATTG, where the superconducting order couples with a magnetic order29 within an energy scale of ~200 mK. Aspects of this competing order will be further seen in measurements with in-plane magnetic fields later in this Article. First, we note the evolution of the switching distribution beyond 200 mK (Fig. 2d) when the distributions get wider and subsequently develop a substructure. As discussed next, this provides an insight into the spatial structure of the superconductor.
Spatial inhomogeneities in the LAO/STO system lead to the creation of weak links between the superconducting parts of the system, which, in turn, create an array of JJs16. This description of an array of JJs is also suitable for MATTG owing to the moiré inhomogeneities present in the system13 and is further supported by our switching measurements that illustrate the stochastic nature of Is, which is a characteristic of JJs24,30,31. The array of the JJ-coupled superconducting islands can be modelled to an equivalent resistively and capacitively shunted junction circuit. The particle in the washboard potential landscape can escape either by a macroscopic quantum tunnelling (MQT) or a thermal activation (TA) process (Fig. 2f, inset). The system can undergo a transition to a lower-energy state by thermal excitations over the intervening barrier at sufficiently high temperatures. However, at lower temperatures, the transition across the barrier occurs via quantum mechanical tunnelling—a process independent of temperature. The histograms’ standard deviation (σ) showcases this temperature dependence for both processes, allowing us to extract the microscopic information. The categorization of the system in either of these regimes is done by noting the standard deviation divided by the mean switching current \(\sigma /{I}_{{\rm{s}}}^{{\rm{mean}}}\) of the switching distribution as a function of temperature (Fig. 2f). We can note that \(\sigma /{I}_{{\rm{s}}}^{{\rm{mean}}}\) remains weakly dependent on temperature, a characteristic of MQT, up to 1 K. Thereafter, \(\sigma /{I}_{{\rm{s}}}^{{\rm{mean}}}\) increases with temperature, indicating a transition into the TA regime. The temperature of this transition is called the cross-over temperature TCO and is around 1 K for this system (Supplementary Section XII provides additional measurements showing the suppression of TCO on the application of a small finite perpendicular magnetic field). A similar transition from the MQT to TA regime is also noted in graphene-based JJs23. We also use the resistively and capacitively shunted junction model to analyse the MATTG as an array of JJs, and estimate the shunt capacitance C to be C ≃ 1.3 fF (Supplementary Section XI). This value of capacitance allows an independent cross-check of the TCO in the system (Supplementary Section XII). All these evidences show that we can visualize the system as a JJ network.
The switching distribution histograms also develop a substructure at temperatures above 1 K—peaked at two current values (Fig. 2d, blue-coloured histogram). The different twist angles in the device host different \({I}_{s}^{{\rm{mean}}}\) values due to relaxation-induced moiré inhomogeneities and are separated out by increasing the temperature resulting in the double-peaked distribution. As the temperature increases further, beyond 1 K, the bimodal distribution gradually evolves into a broad distribution without much substructure at 2 K (Supplementary Section X-D). The bimodal distributions seen at higher temperatures further add to the list of evidence in support of the claim that MATTG is an inhomogeneous superconductor with regions of the superconductor separated by moiré solitons and twistons13. This inhomogeneous nature of the system, we believe, could only be brought out by studying large statistics of switching events.
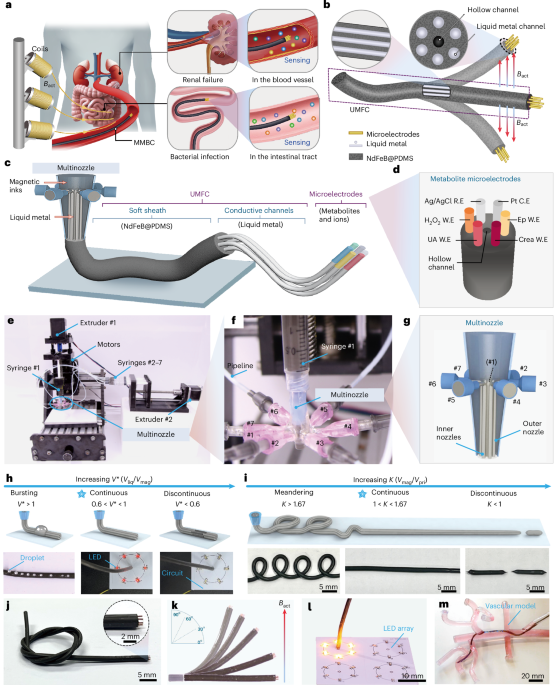
As we discussed earlier, we observe a non-monotonic variation in \({I}_{\rm{s}}^{{\rm{mean}}}\) with temperature—an aspect we attributed to possible competition between the superconducting and magnetic orders. We now probe the possibility of magnetic order using an in-plane magnetic field B∥ (ref. 32) by studying the evolution of the switching distribution in B∥. Figure 3a,b shows the switching histograms from –1 T to 1 T and vice versa, plotted at a bin of 0.1 T (Extended Data Fig. 1 shows the corresponding three-dimensional plot of the histograms). The distributions for magnetic fields of 1 T and –1 T differ from each other in their \({I}_{\rm{s}}^{{\rm{mean}}}\) values for both directions of field sweep (Fig. 3c,d). This brings out the striking difference in the response of the system to the direction of the magnetic field—second evidence for competing order that we provide using switching measurements (Supplementary Section XIII shows the additional thermal cycling data of switching histograms in the presence and absence of an in-plane magnetic field). Such a behaviour can be attributed to a combination of spin-singlet and spin-triplet configuration in the system6, or competing orders in the vicinity of the superconducting order7,8,11,29; this makes MATTG a potential platform to study competition between a superconducting order and a magnetic order.
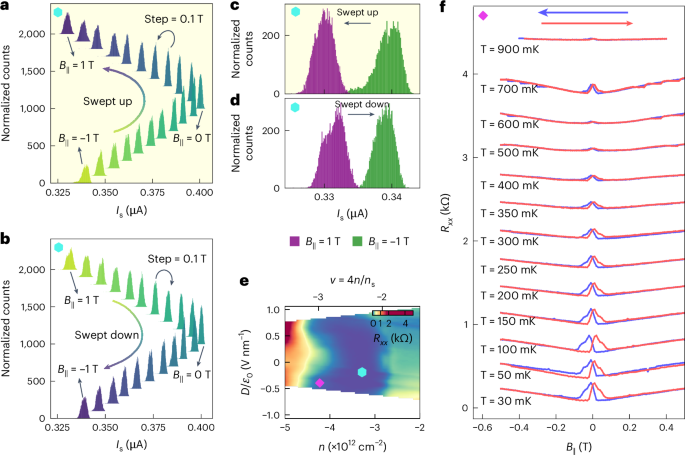
a,b, Switching histograms at optimal hole-side doping and electric field at T = 20 mK, as a function of the in-plane magnetic field B∥ up to ±1 T in the up-sweep (a) and down-sweep (b) directions. The distributions show the magnetic-field-direction-dependent response. The arrows represent the direction of B∥ sweep. The histograms are shown in distinct colours for clarity. Yellow indicates the data collected first, whereas blue represents the data collected last. Each histogram is shifted along the y axis by 100 counts for clarity. c,d, Switching histograms at 1 T and –1 T for the field swept up (c) and swept down (d), pointing out the direction-dependent response of the device to B∥ in that the switching current Is is different for 1 T and –1 T. e, Plot of the longitudinal resistance Rxx in the n–D parameter space, zoomed in near the hole-side superconducting region. The switching data in a–d are taken at the hole-side superconducting region marked by a cyan hexagon. A normal (Rxx ≠ 0) region is marked by a magenta diamond, and identifies the doping and electric field at which the data in f are acquired. f, Longitudinal resistance Rxx plotted as a function of the in-plane magnetic field B∥, at a doping and electric field identified by a magenta diamond in e and marks the phase in the neighbourhood of the superconducting phase. We observe butterfly hysteresis features that evolve and subsequently vanish with increasing temperature. The arrows specify the direction of B∥ sweep. Plots at each temperature are shifted along the y axis by 0.3 kΩ for clarity.
Source data
Figure 3e marks the superconducting region in which the switching experiments are performed and the neighbouring region in which a magnetic order is probably present—this uses our second technique distinct from the switching measurements. It is interesting to note from Fig. 3f that the longitudinal resistance Rxx in the vicinity of the superconducting phase in the n–D phase diagram shows a hysteretic behaviour with the in-plane magnetic field B∥. The hysteretic response dies out with temperature and is absent from 900 mK. We do not, however, understand the re-emergence of hysteresis at 700 mK. Next, we discuss the key aspects of our observation of magnetic hysteresis in longitudinal resistance.
In Fig. 3f, we see the hysteresis in longitudinal resistance as one dopes the system away from the superconducting region (Extended Data Fig. 2). First, the hysteresis is pronounced with an in-plane magnetic field, whereas it is subtle but observable with a perpendicular magnetic field (Extended Data Fig. 2 shows the data for Rxx, and Supplementary Section XIV provides the data for Hall resistance). Second, the hysteresis with an in-plane magnetic field is accompanied by a substantial magnetoresistance (~50% for a field up to ~0.5 T). Last, the hysteresis and magnetoresistance disappear at temperatures of ~900 mK (Extended Data Fig. 3), indicating a common origin for the distinct observations of hysteresis and magnetoresistance. Additionally, in samples that do not show the superconducting response, the hysteresis and magnetoresistance are still present (Extended Data Figs. 4 and 5). The observed hysteresis may be ascribed to multiple phenomena, stemming from the presence of localized magnetic moments within the MATTG sample. Although more complementary techniques are required to understand the exact mechanism, spin flip, spin relaxation and heating due to local moments in the system are some of the possible mechanisms driving the observed hysteresis features.
The magnetoresistance with an in-plane field in MATTG is positive and largely linear with the field—which is remarkable. In high-Tc superconductors, such an observation of positive magnetoresistance with an in-plane field is attributed to the superconducting fluctuations33, whereas in a magnetic material, it can be attributed to spin fluctuations34. Thus, a linear magnetoresistance in MATTG with an in-plane magnetic field probably points to a magnetic origin in the system. As stated before, the correlated appearance of hysteresis and magnetoresistance in the system points to a common origin, with each of them individually pointing strongly to the presence of a magnetic order in the system. Thus, our switching data, together with the longitudinal magnetoresistance, provide strong evidence for the proximal magnetic and superconducting orders. Additionally, we observe the superconducting diode effect in our MATTG devices with a current asymmetry of ~1.2% (Supplementary Section XV), suggesting time-reversal symmetry breaking consistent with our direct observations. The non-zero asymmetry is consistent with the presence of a competing magnetic order, as discussed next35. The superconducting diode effect refers to the asymmetry in Is for the positive and negative current biases; it suggests the breaking of time-reversal and inversion symmetries. A zero-field diode effect has been reported in twisted trilayer graphene on a WSe2 heterostructure36. Our observation is consistent with past works that indicate time-reversal symmetry breaking in MATTG, which we claim is due to the presence of a magnetic order.
MATTG is a two-dimensional system and is expected to undergo a BKT transition, derived within the clean XY model; this forms the motivation to study the evolution of the superconducting phase in MATTG. We expect to observe a discontinuous jump in superfluid stiffness \({J}_{{\rm{s}}}({T}_{{\rm{BKT}}}^{-})=\frac{2}{\uppi }{T}_{{\rm{BKT}}} \,{\rm{and}}\,{J}_{{\rm{s}}}({T}_{{\rm{BKT}}}^{\;+})=0\) in the clean limit, where TBKT is the BKT transition temperature and \({T}_{{\rm{BKT}}}^{-}\) and \({T}_{{\rm{BKT}}}^{\;+}\) are temperatures just before and after the transition, respectively. It is also related to a nonlinear exponent in the Vd.c.–Id.c. curves and allows us to estimate Js in such systems18:
$$V\propto {I}^{\alpha (T\;)},\alpha (T\;)=1+\frac{\uppi {J}_{{\rm{s}}}(T)}{T}.$$
(1)
The corresponding jump in α, \(\alpha ({T}_{{\rm{BKT}}}^{-})=3,\,\alpha ({T}_{{\rm{BKT}}}^{+})=1\), is used to characterize the BKT transition temperature in two-dimensional twisted graphene heterostructures exhibiting SC. However, this description holds true for a clean limit of the sample. In disordered samples, the Js value is strongly suppressed, giving rise to a fragile superconducting condensate, like has been reported in LAO/STO systems. The disorder gives rise to spatially isolated puddles of superconducting regions and connects to the inhomogeneous superconductor picture, arising from relaxation-induced moiré inhomogeneities in MATTG presented earlier.
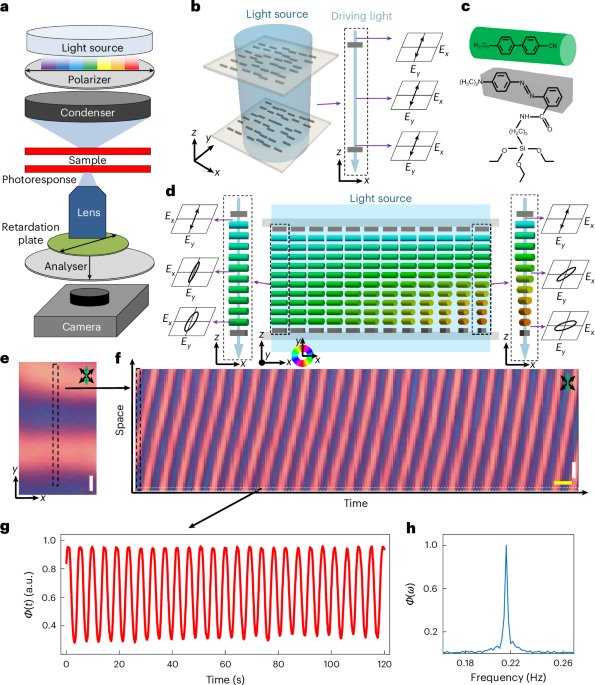
Estimating Js in such systems with mesoscopic-scale moiré inhomogeneities is challenging owing to the small dimension of samples as well as the broadening of the BKT transition due to the inhomogeneities17,18. An important and overlooked consideration in this analysis is that the current biases at which α is extracted must be about an order of magnitude smaller than the typical Is value. At lower currents, the exponent captures the vortex–antivortex depairing central to BKT physics rather than the depairing of Cooper pairs close to Is. We extract α from the Vintegrated versus Id.c. curves at low currents (Fig. 4a and Supplementary Section XVI-A). We observe a strong suppression of α (always less than 3) and no sharp transition in Fig. 4b. The obtained Js values are comparable with the values reported for twisted bilayer graphene in ref. 37 and align with the results from the recent measurements of superfluid stiffness using radio-frequency techniques38,39 (Supplementary Section XVI-B provides a comparison with other works). We do not fully understand the behaviour of Js with temperature; however, the absence of a sharp transition suggests that moiré inhomogeneities indeed play an important role in the kind of physics observed in MATTG SC. In the low-temperature range below 0.5 K, finite-size effects and the competition of magnetic order within the system may result in deviations in Js estimates.
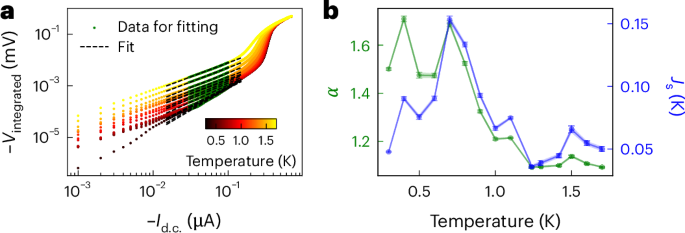
a, Integrated dV/dI curves to produce Vintegrated versus Id.c. curves, at different temperatures; these are separate measurements from the switching measurements. The green data points represent the range used for fitting the nonlinear exponent α, corresponding to low current values of around 50 nA. The black dashed lines show linear fits on a log–log scale: log[|Vintegrated|] = αlog[|Id.c.|]. b, Extracted values of the exponent α (green; left axis) and superfluid stiffness Js (blue; right axis) as functions of temperature. The exponents are extracted from the fits in a. The absence of a sharp jump in α indicates a broadened BKT transition. The error bars are calculated as the standard deviation from the fits.
Source data
We use switching measurements to characterize the MATTG superconductor and magnetoresistance in the proximal normal phase. Our technique gives a direct insight into the spatial moiré inhomogeneities and the competing orders in the system7,8,29,40,41, reflected in the switching response and magnetoresistance as a function of temperature and in-plane magnetic field. Although we show direct evidence of a magnetic competing order, the origin is clearly from an order that couples to the parallel magnetic field. The normal-state hysteretic magnetic response could arise from localized moments. Our experiments provide credence for the heavy-fermion description for the MATTG with a localized moment. In addition, our experimental findings will constrain the possible correlated magnetic states that emerge from the intervalley-coherent order8. Similar phenomenology is also found in complex oxide systems (LAO/STO and KTaO3) hosting superconducting and magnetic orders42,43. In light of this, our work with MATTG possesses important implications that extend beyond the realm of the graphene twistronics community. As we advance, it may be possible to probe the quantum phase transition as one transits from the normal magnetic state to the superconducting state with coexisting magnetic order.